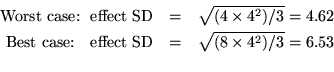Next: Effect size random and
Up: Help for ANOVA Power
Previous: Interface mechanics
Subsections
The dialogs focus on the power of an F test, which in turn depends
(among other things) on the effect size corresponding to some
alternative hypothesis of interest. We quantify effect size to be
the standard deviation of the effects in the ANOVA model; this choice
is made for two reasons:
- It has a meaningful interpretation for fixed, random,
and mixed effects.
- It has the same units of measurement (centimeters, seconds, etc.)
as the data.
In spite of these advantages, there is also some potential confusion,
as is warned earlier in this document.
To illustrate the underlying ideas, consider a two-way completely
randomized factorial design. Specifically, following an example
in Kuehl (1994), page 164, suppose
that we wish to do an experiment to study the effects of aggregate type
and kneading on the tensile strength of asphaltic concrete.![[*]](/icons/foot_motif.gif) The factors and levels are
The factors and levels are
| Factor |
Levels |
|---|
| Aggregate type |
Basalt, Silicious |
| Kneading |
Static, Regular, Low, Very low |
and the response variable is tensile strength, in pounds per square inch (psi).
To determine effect sizes, we have to talk about goals for the experiment.
In this case, we might consider anything less than a 10% difference
to be fairly negligible, so a reasonable goal might be to be able to
detect a 10% difference between two means with reasonable power.
Supposing that we know from experience that the tensile strength will be in
the range of 80 psi, then this goal translates to a difference of about 8 psi.
For Aggregate Type, then, we would want to have the capability of
detecting a difference if, hypothetically, the mean strengths are 76 psi
and 84 psi (or vice versa). To get the corresponding effect size, first
subtract the overall mean (thus obtaining -4 and +4); these represent
the hypothetical effects of aggregate type. The effect SD to
enter in the dialog is defined as
| 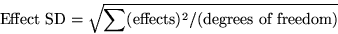 |
(1) |
So the desired effect SD for aggregate type is
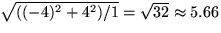 psi.
psi.
The thinking is a little more complicated when determining an
effect size for Kneading. Supposing that we still want to detect differences
of 8 psi or so between two means, there are several different
corresponding scenarios. The effects could be {-4,+4,0,0},
or {-4,-4,+4,+4}, or {-4,-2,+2,+4},
or a variety of other possibilities
(again, the order of these effects is unimportant). Noting that this
four-level factor has 3 degrees of freedom and
applying Equation (3.2), the corresponding
effect SDs are 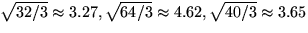 , respectively. It can be shown that the first
two values are the minimum and maximum possible values, representing
worst- and best-case scenarios. We might want to try all three of these
effect SDs in the dialog to see what the range of power is.
, respectively. It can be shown that the first
two values are the minimum and maximum possible values, representing
worst- and best-case scenarios. We might want to try all three of these
effect SDs in the dialog to see what the range of power is.
Now, consider the interaction. Perhaps you do not want to have any goals
at all for the interaction, in which case you can just ignore it. Otherwise,
it may be useful to think in terms of ``simple effects,'' i.e.,
comparisons within a row or column. Here are two scenarios of
interaction effects for the concrete example:
These represent the worst and best-case scenarios, respectively,
when some simple comparisons are as large as 8 psi. Note that every
row and every column of each table sums to 0; otherwise, main
effects would be in force and we would not have pure interaction
effects. The effect SDs are again calculated using Equation (3.2),
noting that the interaction has 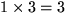 degrees of freedom:
degrees of freedom:
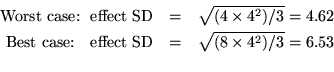
We recognize that the above methods are somewhat tedious. To aid in
obtaining effect sizes for fixed effects and their interactions, an
Effect Advisor application is available via the Options menu.
It opens with a dialog where you choose the number of rows and columns
to study; then, after clicking on ``OK'', the window is redrawn with
data-entry fields for hypothetical cell means, marginal means,
effect SDs, and effect ranges. The Effect Advisor dialog for our
example (2 rows, 4 columns), looks like this:
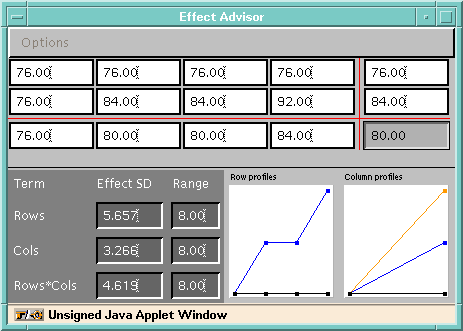
If you change the value in any field and
hit Enter or click elsewhere, all the other fields are updated
appropriately. In addition, there are items in the Options menu
to choose minimum-SD, maximum-SD, or linear effects (holding
the range fixed) for rows, columns, and interaction. The above
illustration was obtained by selecting minimum SDs for each term,
setting all the ranges to 8.00, and setting the grand mean to 80.
Note that the
effect SDs shown are consistent with the minimum SDs obtained above.
The interaction plots give a visual idea of these target effects.
The Effect Advisor is only set up for two factors. You can study
more factors by working with two of them at a time (but there is
no provision for interactions of higher order than 2). To study
just one factor, just ignore either rows or columns and work with
the marginal means of one factor.
Power cannot be determined without knowledge of the SD of the
experimental error (and in general, the SDs of all sources of random error).
Often, information about experimental error is estimated from a pilot
study, or from past experiments with perhaps a different design
but the same response variable and same structure of replications.
In the concrete example, suppose that we already have several specimens
of concrete in the laboratory, all made from different batches but
with the same ``recipe'' and kneading method. Thus, it is thought
that the variations in tensile strength of these specimens are
reasonably representative of the within-cell variations we can expect
in the planned experiment. Seven of these specimens are tested,
and we find that the sample variance is 12.50 (so that the SD is 3.54).
We may use 3.54 as an estimate of the within-cell SD in the power analysis.
This is only an estimate; the true SD may be larger or smaller than this.
When estimates are used (i.e., essentially always), the powers of tests
are only estimates of the true powers. Power analysis is not an exact
science, but it is a way of finding a reasonable sample size relative
to the goals of a study.
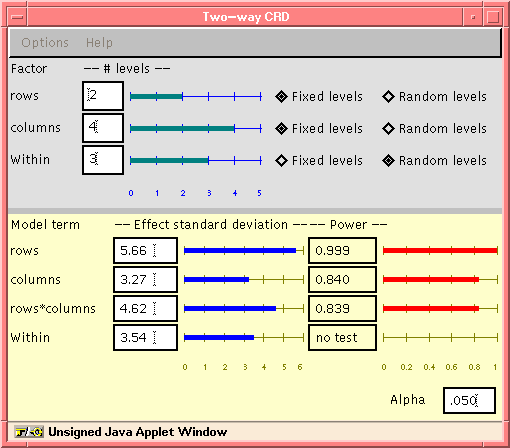
Now it's time to run the Java applet for planning the experiment.
The dialog is shown below with the effect sizes computed above
entered (the worst-case effect SDs are used for the Kneading and
interaction terms). We also have to enter the correct numbers of
levels for Aggregate type (``row''in the dialog) and Kneading
(``column'' in the dialog).
The idea of determining sample size is to manipulate it and observe
the powers of the tests of interest until acceptable results are
achieved.
At the .05 significance level (the default), a sample size of 3
observations per cell is sufficient to provide power exceeding 80%
for all three goal values.
(Note that sample size is inputted as the number of levels for ``Within.'')
We therefore recommend that an
experiment with 3 observations per cell (24 observations total)
be conducted. The list of 24 factor combinations (3 copies of
each) is arranged in random order to determine the protocol
for a completely randomized experiment.
Incidentally, a power of 75-80% is often used as a target;
a lower power than that does not provide a good chance of detecting
the stated effect, and powers of 95% and higher usually
require about twice as much data--wasting time, money, resources, and
experimental animals' lives.
It is instructive to try out some variatioins on this example.
Using a Java-capable web browser, connect to
http://www.stat.uiowa.edu/~rlenth/Power/TwoWay.html
.
Here are some things to try:
- 1.
- Reproduce the results above.
- 2.
- What happens to the powers of the tests if the sample size
is reduced to 2 observations per cell? Increased to 4?
- 3.
- What happens if you change alpha to .01?
- 4.
- What effect SD for rows can be detected with a power of .80?
(Suggestion: drag on the effect-SD bar and watch the power bar.)
What difference of means has this effect SD?
(You'll have to do some math.)
Often, the sample size is essentially determined by the budget, and
such manipulations give us a measure of the capability of the experiment.
- 5.
- Use the options menu, obtain a report of the current state
of the power analysis.



Next: Effect size random and
Up: Help for ANOVA Power
Previous: Interface mechanics
Russ Lenth
6/3/1998
![]() , respectively. It can be shown that the first
two values are the minimum and maximum possible values, representing
worst- and best-case scenarios. We might want to try all three of these
effect SDs in the dialog to see what the range of power is.
, respectively. It can be shown that the first
two values are the minimum and maximum possible values, representing
worst- and best-case scenarios. We might want to try all three of these
effect SDs in the dialog to see what the range of power is.