- a.
- The derivative of the log likelihood is
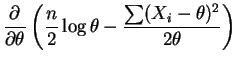
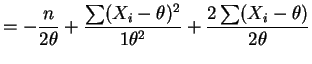
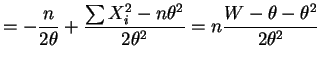
So the MLE is a root of the quadratic equation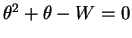 .
The roots are
.
The roots are
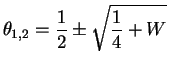
The MLE is the larger root since that represents a local maximum and since the smaller root is negative. - b.
- The Fisher information is
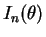
![$\displaystyle = -nE\left[\frac{\partial}{\partial\theta}\left(\frac{\theta^2 + \theta - W} {2\theta^2}\right)\right]$](img604.png)
![$\displaystyle = \frac{n E[W]}{\theta^3} - \frac{n}{2\theta^2} = n \frac{E[W] - \theta/2}{\theta^3}$](img605.png)
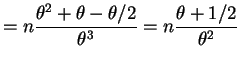
So AN
AN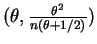 .
.
The UMVUE of
![]() is
is
![]() and
the MLE is
and
the MLE is
![]() . Since
. Since
both
In finite samples one can argue that the UMVUE should be preferred if unbiasedness is deemed important. The MLE is always larger than the UMVUE in this case, which might in some contexts be an argument for using the UMVUE. A comparison of mean square errors might be useful.
For the data provided,
![]() and
and
![]() .
.
Solution: The log-likelihood is
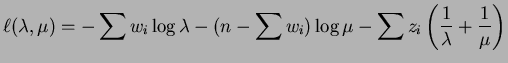 |
So
 |
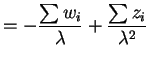 |
|
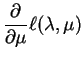 |
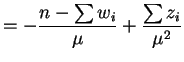 |
|
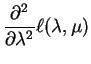 |
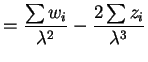 |
|
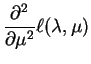 |
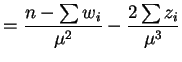 |
|
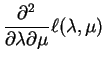 |
||
 |
||
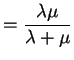 |
So
![$\displaystyle E\left[-\frac{\partial^{2}}{\partial\lambda^{2}}\ell(\lambda,\mu)\right]$](img630.png) |
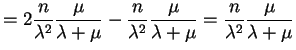 |
|
![$\displaystyle E\left[-\frac{\partial^{2}}{\partial\mu^{2}}\ell(\lambda,\mu)\right]$](img632.png) |
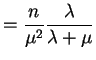 |
and thus
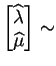 AN AN |
Solution: The MLE's are
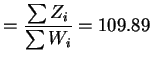 |
||
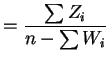 |
The observed information is
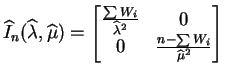 |
Thus the marginal posterior distribution of
So
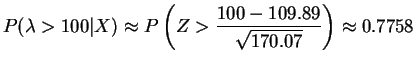 |
