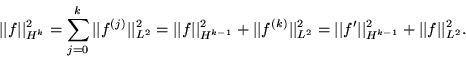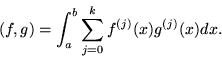Function spaces

  In order to analyze the finite element method, it helps to have an understanding of function spaces. These are not only sets of functions, but they typically have a norm associated with them. The most common, and most useful, function spaces are listed below.

Name Description Norm

$$\vert\vert f\vert\vert _\infty=\max_x\vert f(x)\vert$$ C[a,b] Continuous functions on [a,b]

$$\int\vert f(x)\vert dx<+\infty \vert\vert f\vert\vert _{L^1}=\int\vert f(x)\vert dx$$ L¹(a,b)

$$\int\vert f(x)\vert^2 dx<+\infty \vert\vert f\vert\vert _{L^2}=[\int\vert f(x)\vert^2 dx]^{1/2}$$ L²(a,b)

$$p\ge1 \int\vert f(x)\vert^p dx<+\infty \vert\vert f\vert\vert _{L^p}=[\int\vert f(x)\vert^p dx]^{1/p}$$ L^p(a,b)

$$f\in L^2 f'\in L^2$$ H1(a,b) ||f||H12=||f(x)||L22+||f'(x)||L22

Complete spaces and Cauchy sequences

In the abstract, we will be dealing with a set of functions X with a norm $\vert\vert\cdot\vert\vert$.So far, we don't know what to do with limits of objects x_k in X.

If we were talking about real numbers, we would expect that a sequence like 1, 1.4, 1.41, 1.414, 1.4142, 1.41421, ...would converge. If our universe only consisted of rational numbers, then we would be in trouble because they could be converging to $\sqrt{2}=1.414213562373\dots$, which is not rational. But with real numbers, any sequence like 1, 1.4, 1.41, 1.414, 1.4142, 1.41421, ..., which adds one new digit with each element in the sequence, converges.

What sequences x_k in a set X with norm $\vert\vert\cdot\vert\vert$ ``ought'' to converge? The answer that we use is the idea of a Cauchy sequence:

A sequence x_k is a Cauchy sequence if for every $\epsilon\gt$ there is an N such that $k,l\ge N$ implies $\vert\vert x_k-x_l\vert\vert<\epsilon$.

A space (consisting of X with norm $\vert\vert\cdot\vert\vert$) is complete if every Cauchy sequence has a limit.

The first example of a complete space is the real line.

The first example of a complete function space that most people meet is the space of continuous functions on [a,b], denoted C[a,b], with norm $\vert\vert f\vert\vert _\infty=\max_x\vert f(x)\vert$.

All of the examples from §2 are complete function spaces.

Complete normed spaces are called Banach spaces after the Polish mathematician, Stefan Banach.

L²(a,b) -- square integrable functions

One of the most important function spaces is L²(a,b) - the space of square integrable functions on the interval (a,b). The L² norm is $\vert\vert f\vert\vert _{L^2}=[\int_a^b\vert f(x)\vert^2 dx]^{1/2}$.

The precise definition of L²(a,b) is based on Lebesgue integration theory, which is beyond the scope of these notes. The trickiest aspect of L²(a,b) is that we cannot distinguish between functions in L²(a,b) that differ only at a single point, or at a countable number of points.

[Technically, we regard f=g if the set $\{ x\mid f(x)\ne g(x) \}$is a null set; that is, if changing the values of this set has no effect on any integrals.]

One of the more important aspects of L²(a,b) is that the norm comes from an inner product:

$$(f,g) = \int_a^b f(x) g(x) dx$$

for real-valued functions. This inner product has the properties that we need for an inner product:

1.

$(f,f)\ge0$ and is zero only if f=0

2.

(f,g) = (g,f)

3.

for any scalars (constants) a and b, and functions f and g, $(f,a\cdot g + b\cdot h) = a (f,g)+b (f,h)$.

The corresponding norm (like the L² norm) is given by

$$\vert\vert f\vert\vert = \sqrt{(f,f)}.$$

Now we will see the Cauchy inequality holds for these inner-product spaces:

$$\vert(f,g)\vert \le \vert\vert f\vert\vert \vert\vert g\vert\vert.$$

Proof. For any a, $(f+a.g,f+a.g)\ge0$, so the quadratic in a,

$$(f,f) + 2a(f,g) + a^2(g,g)\ge 0.$$

This means that the quadratic has at most one (repeated) real root. This means that either (g,g)=0, or the discriminant (``b²-4ac'') cannot be positive. In the first case, ||g||=0, so g=0, and there is nothing to show. In the second case, $4(f,g)^2-4(f,f)(g,g)\le0$.That is, $\vert(f,g)\vert\le \vert\vert f\vert\vert \vert\vert g\vert\vert$ as required.     QED.

This makes L²(a,b) an example of a complete inner product space, or as it is better known, L²(a,b) is a Hilbert space.

Since functions in L²(a,b) are integrable, they represent distributions; L² is a subset of the space of distributions.

Sobolev spaces H¹(a,b), etc.

Sobolev spaces are Banach spaces where the norm involves derivatives, or at least, something other than just function values. The simplest of these is H¹(a,b).

H¹(a,b) is the Banach space of functions

$$\left\{ f\mid f\in L^2(a,b),\; f'\in L^2(a,b) \right\}$$

with the norm

||f||H12 = ||f||L22 + ||f'||L22.

Actually, we need to be a little careful about ``$f'\in L^2(a,b)$'', since we need to keep a tight connection between f and f'. For example, if we think of the Heaviside function H(x) of §1.1, H'(x)=0 for all x, except for x=0, where it is undefined. Thus as far as integrals are concerned, we cannot distinguish between H'(x) and the zero function. On the other hand, H(x) is definitely not constant. So we would like to keep this function out of the Sobolev space H¹(a,b).

There are two ways of avoiding functions like H(x):

1.

We can require that f is absolutely continuous: $f(y) = f(x) + \int_x^y f'(z) dz$. This will work in one space dimension, but not in more dimensions.

2.

We can require that the distributional derivative f' of f belong to L²(a,b) as a subset of distributions. This works in any number of dimensions, but is more abstract.

The $\delta$-function is not in L²(a,b) if a<0<b: the indefinite integral of any function in L² is continuous (in fact, absolutely continuous), while H(x) clearly is not. Thus $H'=\delta\notin L^2(a,b)$, and so H is not in H¹(a,b).

The Sobolev space H¹(a,b) has an inner product that defines the norm:

$$(f,g) = \int_a^b(f(x) g(x)+f'(x) g'(x)) dx.$$

Higher order Sobolev spaces can be defined:

$$H^k(a,b) = \left\{ f\mid f, f', \dots, f^{(k)}\in L^2(a,b) \right\}$$

with the norm

$$\vert\vert f\vert\vert _{H^k}^2 = \sum_{j=0}^k \vert\vert f^... ...t f'\vert\vert _{H^{k-1}}^2 + \vert\vert f\vert\vert _{L^2}^2.$$

The corresponding inner product is

$$(f,g) = \int_a^b\sum_{j=0}^k f^{(j)}(x) g^{(j)}(x) dx.$$