Exponential Running Time

A function f(n) is exponential, if it has the form a×bn, where a and b are some constants. For example, 2n, is an exponential function. A program or a function that has exponential running time is bad news because such programs run extremely slowly!

Example. Suppose the running time of a function is 2n. Further suppose that each primitive operation can be executed in one micro second (i.e., 10-6 seconds). Then solving the problem for n equals 100 will take 10-6×2100 seconds. This equals 1.26765×1024 seconds, which is more than 10,000 trillion years, more than the lifetime of the universe by several orders of magnitude. You get the point. The function starts innocuously enough but grows extremely rapidly and reaches astronomical proportions very quickly and for a fairly small value of n. Programs or functions whose running time is exponential can be useful only for tiny inputs.

It turns out that the recursive fibonacci number function, given below, has running time that is exponential. 

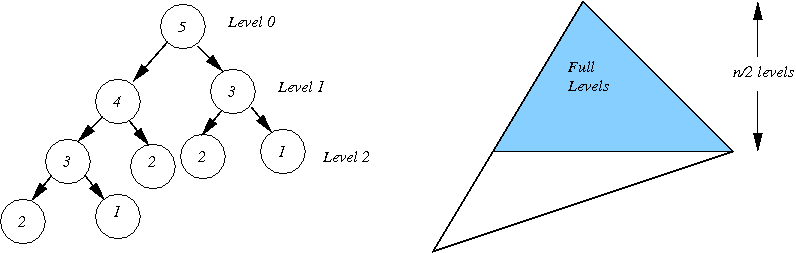
	def fibonacci(n):
		if((n==1) or (n==2)):
			return  1
		if(n > 2):
			return fibonacci(n-1) + fibonacci(n-2)
Here is a figure (on the left) showing the recursion tree when fibonacci is called with n equals 5.

graph 1

To estimate the running time of the function fibonacci when it is called with arbitrary n, we first note that in order to do this it is sufficient to simply count the total number of function calls to fibonacci that are made. When n equals 5, you can count the number of "nodes" in the recursion tree on the left, to conclude that a total of 9 function calls were made. It is sufficient to count the number of function calls because, the running time of the function fibonacci, is a constant, if we exclude the time spent inside recursive calls.

To count the number of nodes in the recursion tree corresponding to fibonacci(n), look at the shape of the recursion tree on the right. A level i is called full if it has 2i nodes in it. In the recursion tree for fibonacci(5), levels 0, 1, and 2 are full. For the tree on the right, levels 0 through n/2-1 are all full. Level n/2-1 has 2n/2-1 nodes. Therefore the tree has at least 2n/2-1 nodes. A bit of simplification shows that this is 1/2×SquareRoot(2)n, which is roughly 1/2×(1.414)n. Note that this is an underestimate on the actual number of nodes in the tree, but suffices to show that the running time of the fibonacci(n) function is at least exponential in n.

It is of course quite easy to see that the iterative fibonacci function, shown below, runs in O(n) time. 

	def iterativeFibonacci(n):
		if((n==1) or (n==2)):
			return 1

		previous = 1
		current = 1
		count = 2
		while(count < n):
			temp = current
			current = current + previous
			previous = temp
			count = count + 1

		return current