(a) code: a part of SmallList.cxx (also need to modify SmallList.h)
void SmallList::makeRandomList(int n){
assert(n <= MAX_SIZE);
RandGen rnd(n);
for(int i = 0; i < n; i++)
myList[i] = rnd.RandInt(1,n);
mySize = n;
}
(b) code: a part of test_CountDistinct.cxx
//****************************************************************************
// g++ -c rando.cxx -o rando.o
// g++ -c SmallList.cxx -o SmallList.o
// g++ test_CountDistinct.cxx SmallList.o rando.o -o test_CountDistinct
// test_CountDistinct
//****************************************************************************
#include <cstdlib>
#include <iostream>
#include "SmallList.h"
using namespace std;
int CountDistinct(int n) {
SmallList list;
list.makeRandomList(n);
list.removeDuplicates();
int number;
number = list.size();
return number;
}
int main(){
float count;
for(int n = 100; n <=1000; n+=100){
count = 0.0;
for(int i = 0; i < 10; i++)
count += CountDistinct(n);
cout << count/10 << endl;
}
return EXIT_SUCCESS;
}
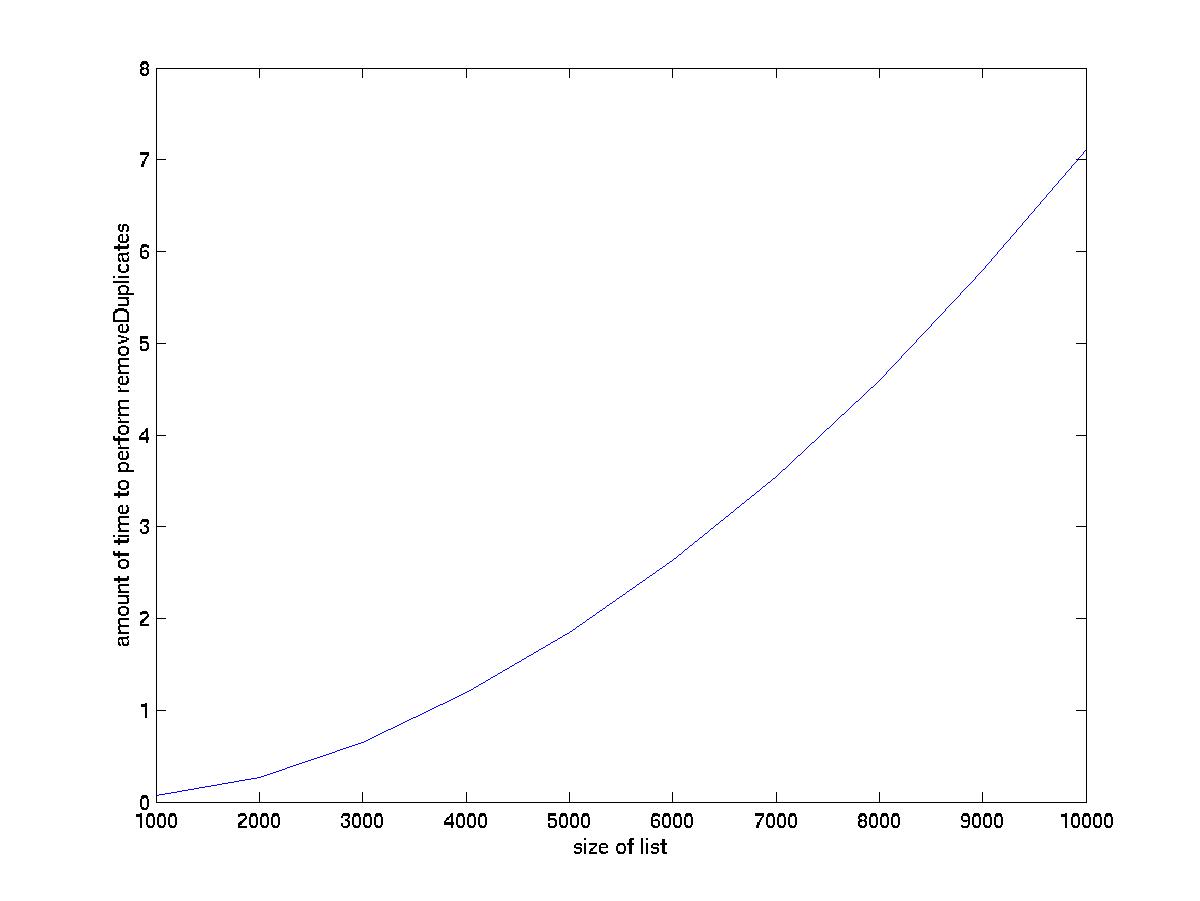
(c) plot
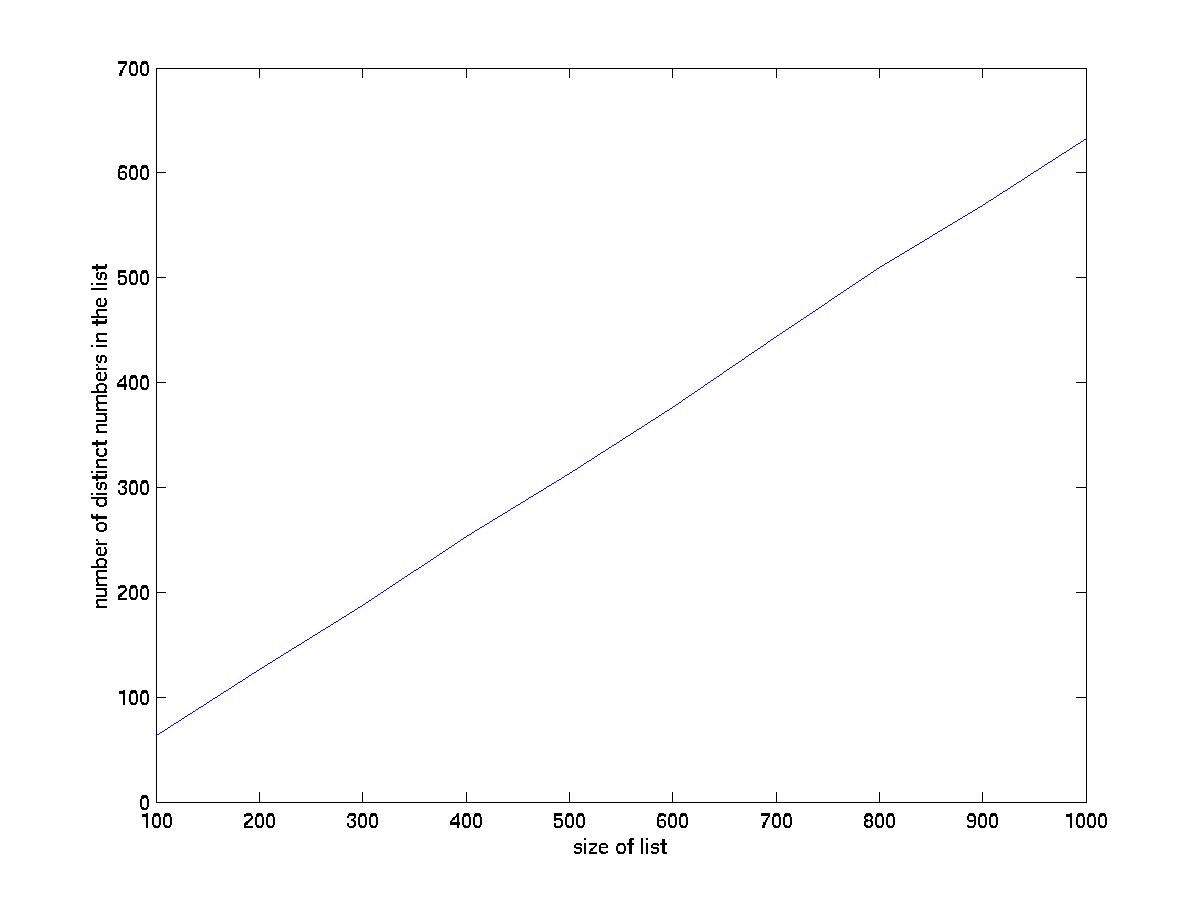
(d) comments on the plot
The number of distinct element increases as the size of list increases. It gives us a straight line. The slope of the straight line tells us that about 60% of the elements in this list are distinct.