- A Set ADT represents some subset of {1, 2, ..., n} for some natural number
n. It supports the operations insert, delete, isMember, isEmpty,
union, and intersection,
which are described below.
- S.insert(x) takes a number x in {1, 2, ..., n} and inserts x it into S.
- S.delete(x) takes a number x in {1, 2, ..., n} and deletes it from S.
- S.isMember(x) takes a number x in {1, 2, ..., n} and returns true if x is in S
and returns false, otherwise.
- S.isEmpty() returns true if S is empty and returns false otherwise.
- S.union(A) takes a subset A of {1, 2, ..., n} and changes S to S union A.
- S.intersection(A) takes a subset A of {1, 2, ..., n} and changes S to S intersection A.
I want you to implement the Set ADT as a boolean array of size n.
If an element x in {1, 2, ..., n} belongs to the set, then slot x-1 in the boolean
array should be true; otherwise it should be false.
-
The posted implementation of the Queue ADT is not dynamic.
In other words, once the array becomes full no more elements can be enqueued.
Modify this implementation to make it dynamic.
Use the usual technique of doubling the array size when the queue becomes full.
-
Show the adjacency matrix representation for the graph shown
below. Specifically, show the contents of the 1-dimensional array of
vertex names and the 2-dimensional boolean array that keeps track of the edges.
You should consult this Graph class for more
details.
Just so that all answers are consistent, I want you to store the names of
the vertices in alphabetical order in the array of vertex names.
Also, show what happens when you delete vertex C.
Specifically, show the new 1-dimensional array of names and
2-dimensional boolean array of edges after vertex C has been deleted.
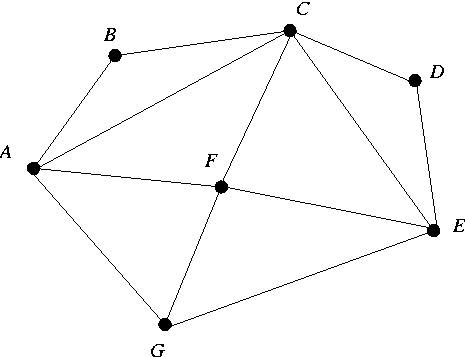
-
Perform breadth-first search with source vertex A on the above
graph using
the implementation discussed in class (and posted on the course
page).
Assume that the getNeighbors method returns vertices in lexicographic order.
Answer the questions below.
-
Show the computed breadth-first search tree.
Mark vertices by the order in which they were discovered.
For example, mark the source vertex 1, it's first neighbor 2, etc.
-
Show the contents of the queue at the beginning of each execution of the
while(!Q.isEmpty()) loop.
-
For this problem, suppose that Lord Darth Vader has tampered with
our implementation of the Queue ADT.
When you perform a dequeue operation, you
don't get the first element from the queue; instead you get the
second element.
Of course, if the queue has only one element, then that is what you get
when you perform a dequeue.
Using the Queue ADT so maliciously tampered by Lord Vader,
perform breadth first search on the graph
shown above, starting first from vertex A
and then starting from vertex B.
For each traversal, show
(i) the order in which vertices are discovered by
breadth first search and (ii) the breadth first search tree.
As usual, assume that the neighbors of each vertex are scanned
in alphabetical order of their names.
-
Write a method of the LinkList class that deletes and returns
the last Link of the linked list. Use the following function header:
public Link deleteLast()
If the linked list is empty, then the function just returns null.
-
Write a method of the myGraph class that determines if a given
pair of vertices have a common neighbor.
The function returns true if the given vertices have a common
neighbor; otherwise it returns false.
Two vertices A and B have a common neighbor if
for some vertex C, the graph contains the edge between A
and C and the edge between B and C.
For simplicity, you may assume that the two given vertices are present
in the graph.
Solve this problem using both the adjacency matrix implemenation
(myGraph class) and the adjacency list representation
(myListGraph class).
-
Consider the STRANGE_QUEUE ADT that is similar to the QUEUE
ADT, except that each item has an associated priority that can be
0 or 1. Items with priority 0 are considered very important and are "served"
before items of priority 1. Like the QUEUE ADT, the
STRANGE_QUEUE ADT also supports the operations insert and delete,
but these operations for the STRANGE_QUEUE ADT pay attention to
the priority of the items.
Here is a description of how insert and delete work for
the STRANGE_QUEUE ADT.
- Insert: Add the given item, with the specified priority,
to the collection.
- Delete: if there is an item with priority 0 in the collection,
delete the oldest item in the collection with priority 0 and return it.
Otherwise, if there is an item with priority 1 in the collection,
delete the oldest item in the collection with priority 1 and return it
Otherwise, the collection is empty and there is nothing to return.
Write a brief description (5-6 lines) of how you would implement
the STRANGE_QUEUE ADT so that the insert and delete functions,
both run in O(1) time.
Your description would have two parts: (1) describing the data structures
you will use for your implementation and (2) how the two operations are
implemented, using these data structures.
