 has an equivalent decimal value
has an equivalent decimal value 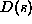 defined as:
defined as:
Introduction
This project asks you to construct a spell checker -- a program that checks and possibly corrects spelling errors in documents.
Overview
As part of this project you will have to write two separate programs: BuildDict.java and SpellCheck.java. As the name suggests, the program BuildDict builds a dictionary of words, while the program SpellCheck uses this dictionary of words to determine which words in a given document are misspelled.
Building a Dictionary
We will build a dictionary by extracting words from large on-line documents known to be error free. I am making available the following six famous novels in text form:
The program BuildDict should read each of these documents, extract words
from them, and insert them into a dictionary.
It is important to have a precise understanding of what we mean by a
word before we proceed.
As far as this project is concerned, a word is a contiguous sequence of 2 or more
letters (lower case or upper case) immediately followed by a non-letter character.
For this project we will ignore the difference between upper and lower case letters
and therefore the words The and the will be considered identical.
To understand the above definition, consider the following text:
The giant telephone company AT&T bought an IBM360 computer last year.
Since then the company has had an error-free run in the telecommunications
industry.
The distinct words extracted from this text are listed below in alphabetical order:
an at bought company computer error free
giant had has ibm in industry last
run since telephone telecommunications the then year
Notice that the word at has been extracted from AT&T and the hyphenated word error-free has contributed two words error and free to the above list. Each of the extracted words needs to be inserted into a data structure that can also be searched quickly (so that the same word is not inserted twice). To support this you should define and implement a class called Dictionary that can be used by BuildDict as well as SpellCheck. You should use hashing with chaining to implement the Dictionary. More on this later. The Dictionary class should contain efficient implementations of the following methods.
The program BuildDict should start by asking the user for a list
of text files to read from.
The user should respond by typing the file names as
[filename1] [white space] [filename2] [white space] [filename3]...In this version of the project you will use the six text files that I have provided. Then BuildDict will read all specified text files and build a dictionary of all distinct words found. It should then write the contents of this dictionary into a file called words.dat. This file constitutes the dictionary that will subsequently be used by the program spellCheck.
The SpellCheck program
After the BuildDict program completes its task and creates the
dictionary file words.dat, the SpellCheck program is ready
to take over.
This program should start by reading the list of words in the
file words.dat into a data structure that can be quickly searched.
You should use the Dictionary class (that was used in BuildDict)
here also.
In addition to the words in words.dat, the program SpellCheck
should add valid single letter words such as A and I to the
dictionary.
After SpellCheck has built the dictionary
it should prompt the user for the name of a document she wants spell-checked.
SpellCheck should then read words from this user specified document,
one-by-one and test if the words appears in its dictionary.
As a running example, suppose that the user wants a file called
myLetter to be spell-checked.
As SpellCheck reads from the file myLetter, it writes into
a file called myLetter.out.
After SpellCheck has completely processed myLetter,
the file myLetter.out will be the corrected version of
myLetter.
Note that myLetter.out is identical to myLetter except
for misspelled words being replaced by correctly spelled words.
The spellCheck program
should make sure that all the white spaces and punctuation marks
that appear in myLetter appear exactly in the same manner in
myLetter.out.
As the program scans the user specified document, it may encounter a word
that is not present in its dictionary.
It assumes that such a word to be misspelled and responds by
(i) displaying the misspelled word and (ii) producing the following prompt:
Do you want to replace (R), replace all (P), ignore (I), ignore all (N), or abort (A)?The user is expected to respond by typing an R, P, I, N, or an A. If the user types anything else, the program should simply ask the question again. Here is what your program should do for each of the possible responses from the user.
What is a hash table?
The idea of a hash table is simple. Let U be the set of all possible strings of lower case letters. Let h: U -> [0,..,M-1] be a function that maps each string in U to a number in the range 0 through M-1. Then any subset S of strings can be stored in an array, let us call this table, of size M by storing a string s in S in slot table[h(s)]. To determine whether a given string s' in U is also in S, we simply compute h(s') and determine if table[h(s')] contains s'. The only problem with this method is that there can be collisions between strings. For example suppose that for two distinct strings s and s' in S, h(s) and h(s') are both equal to some integer k. This means that both s and s' have to be stored in slot table[k]. To handle such a situation, table should be defined not as an array of strings, but as an array of linked lists of strings. The idea is that all strings in S that hash to a particular slot, say k, are stored in the linked list at table[k]. This approach to resolving collisions is called hashing with chaining. The efficiency of this approach depends on making sure that none of the linked lists are too long.
The only aspect of a hash table left to discuss is the hash function h itself.
Any string of lower case letters can be thought of as a number in base-26 by thinking of each
letter as the number obtained by subtracting 97 (the ASCII value of 'a') from the ASCII
value of the letter.
For example, the string next can be thought of as the following base-26 number: 13 4 23 19.
Thus a string  has an equivalent decimal value
has an equivalent decimal value 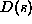 defined as:
defined as:

where 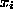 equals the ASCII value of
equals the ASCII value of 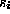 minus 97 for each i,
minus 97 for each i, 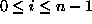 .
Now for any string s define the hash function
h(s) as h(s) = D(s) mod M.
Thus the function h maps any string onto the range 0 though
M-1.
You will have to watch out for possible integer overflow while computing
D(s).
The only thing left to decide is the value of M.
It is common practice to use a hash table whose size is approximately 10 times
the number of items being stored in it.
It is also common practice to choose the size of the hash table to be a prime number.
Use these two thumbrules along with the size of the dictionary, to pick a value for M.
It is critical to the efficiency of a hash table based data structure that
the hash value of the given string be computed extremely efficiently.
There are various tricks one can use to speed up the computation of the hash function
descrcibed above including the use of Horner's rule and bit shifting.
These issues will be discussed in next week's homework.
.
Now for any string s define the hash function
h(s) as h(s) = D(s) mod M.
Thus the function h maps any string onto the range 0 though
M-1.
You will have to watch out for possible integer overflow while computing
D(s).
The only thing left to decide is the value of M.
It is common practice to use a hash table whose size is approximately 10 times
the number of items being stored in it.
It is also common practice to choose the size of the hash table to be a prime number.
Use these two thumbrules along with the size of the dictionary, to pick a value for M.
It is critical to the efficiency of a hash table based data structure that
the hash value of the given string be computed extremely efficiently.
There are various tricks one can use to speed up the computation of the hash function
descrcibed above including the use of Horner's rule and bit shifting.
These issues will be discussed in next week's homework.
What to submit:
You are required to electronically submit by midnight on Monday, 3/20 the following files: BuildDict.java, SpellCheck.java, Dictionary.java, Link.java, and LinkList.java. Make sure that your file names are exactly as above and make sure that you do not submit any additional files.
Final words:
While I have specified quite a few details, I have left enough unspecified so as to leave you with a few design decisions to make. You have 3 weeks for this project because I expect that it will take you 3 weeks! So please start right away.