Problem Set 13. Posted 4/28

Notes: Of the three problems given below, one will be solved by the TAs in next week's discussion section, you will have to solve one in class, and the remaining problem is due in the lecture on Friday, 5/5.

In class we discussed an implementation of Dijkstra's Shortest Path (DSP) algorithm that runs in O(n^2) time on a graph with n vertices. In this problem, you will have to provide an implementation that uses a binary heap. As mentioned in class, such an implementation is much more efficient on sparse graphs and in general runs in O((m+n) log n) time on a graph with n vertices and m edges.
1. For the edge-weighted graph shown below, show the d-values of the vertices obtained by running Dijkstra's Shortest Path algorithm... Also, show a shortest path tree.

2. Modify the myGraph class so that it can represent edge-weighted graphs. Assume that all edge weights are non-negative and use -1 to represent the absence of an edge. Specifically, if Edges[i][j] is -1 then there is no edge between the vertices with indices i and j. This implies minor modifications to many of the functions in the myGraph class. For example, it would make sense to have two versions of the addEdge function, one that takes an edge weight as an argument (in addition to the two endpoints of the edge) and one that does not. The addEdge function that does not take an edge weight as an argument, would add an edge with weight 0 to the graph.

3. Implement the heap-based version of the DSP algorithm as a member function of the myGraph class. Make sure that your implementation constructs a shortest path tree and returns this in an integer array (as we did in the case of a depth first tree and a breadth first tree). The DSP algorithm involves implementing a min-heap and then connecting the graph to the min-heap. A min-heap is just like the heap we have studied in class, except that in a min-heap the element with smallest priority is at the top of the heap. The heap property is "reversed:" the priority of a parent has to be smaller than (or equal to) the priority of each child.

   To connect the vertices in the graph to the heap, maintain an int array called map. This array contains a slot for each vertex in the graph. If a vertex with index i is in the heap, then map[i] contains the slot in the heap that i is in. If a vertex with index i is not in the heap, then map[i] contains -1. Recall that at any time during the running of the DSP algorithm, the vertices in V - S need to be stored in the heap. As the heap changes, map will also have to be updated. However, the updates to map only add a constant overhead to the running time of the heap operations.

   Here are some specifics. Start with Lafore's heap class and modify it into a min-heap. Then add an integer array called map as a data member to this class. Each element that is inserted into the heap comes with two descriptors: a key and a priority. In the case of our application (the DSP algorithm) we insert vertices into the heap and these are decribed by an index (the key) and a d-value (the priority). Also, the DSP algorithm repeatedly calls the change function in the heap class. The change function in the heap class currently takes an index that points to a slot in heapArray. However, for the DSP algorithm, we need a change function that takes as index that points to a slot in map.

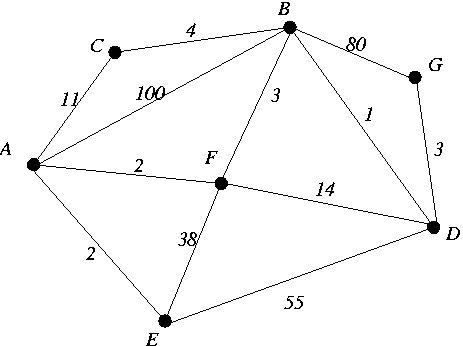
   After implementing the DSP algorithm, run it on the graph shown in Problem 1 and make sure that it computes a correct shortest path tree.

   ---