Problem Set 11. Posted 4/14

Notes: Of the three problems given below, one will be solved by the TAs in next week's discussion section, you will have to solve one in class, and the remaining problem is due in the lecture on Friday, 4/21.

1. Code for the stack based depth first traversal (discussed in class) has been posted here. We also discussed a function called path in class that took a source vertex and a desination vertex and returned a path in the graph from the source vertex to the destination vertex. Here is the function header for path.

   	int[] path(String s, String t)
   

   Recall that if there is no path from the source to the destination, the function returns null.
   1. Add the function path to the myGraph class.
   2. To test this function (and the depth first search function), write a program that builds the Ladders graph (see Problem 2 in Problem Set 5) and then asks the user for two 5-letter English words and responds by printing a ladder from the first word to the second or reporting that such a ladder does not exist. For example, the user might type flour and bread as the two 5-letter words. Your program might respond by printing the sequence of words: flour, floor, flood, blood, brood, broad, bread. I say "might" in the above sentence because there may be several paths in the Ladders graph between flour and bread and it is not guaranteed that your program will print the path shown above.
   3. Are there pairs of words that cannot be reached from each other in the Ladders graph? Write a program that answers the above question and if there are pairs of words that are unreachable from each other in the Ladders graph, reports one such pair. Otherwise your program should simply indicate that no such pairs exist. It is possible to solve this problem by calling the function path one every pair of words. This is terribly inefficient. You can solve this problem by making a single call to the depth first search function.

2. The depthFirstTraversal function written in class is not recursive - it uses an explicitly maintained stack to do backtracking. Write a recursive version of the depthFirstTraversal function that does not use an explicitly maintained stack. The main idea is this: to perform depth first traversal with source s, find an unvisited neighbor, say x of s, and perform depth first traversal with x as source. It may be convenient to think of depthFirstTraversal as a function that initializes data structures (such as visited and dFTTree) and then calls recursiveDepthFirstTraversal. The function recursiveDepthFirstTraversal will be responsible for exploring one connected component of the graph. The function depthFirstTraversal will have to call recursiveDepthFirstTraversal repeatedly for different connected components.

3. For this problem, suppose that Darth Vader has tampered with your implementation of the stack data structure. When you perform a peek or a pop operation, you don't get the top most element from the stack; instead you get the element just below the top most element. Of course, if the stack has only one element, then that is what you get when you perform a peek or a pop.

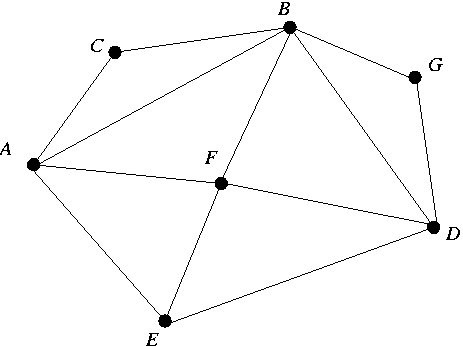
   Using the stack so maliciously tampered by Lord Vader, perform depth first traversal on the graph shown below, starting first from vertex A and then starting from vertex B. For each traversal, show (i) the order in which vertices are discovered by depth first traversal and (ii) the depth first traversal tree. As usual, assume that the neighbors of each vertex are scanned in alphabetical order of their names.

   

   ---