This is a homework assigned in 2004 by Bob Sedgewick and Kevin Payne for an undergraduate class at Princeton. I have made some modifications to it.

Here you are asked to modify our implementation of the classic Dijkstra's shortest path algorithm and optimize it for maps.  Such algorithms are widely used in geographic information systems (GIS) including MapQuest, Google Maps, and GPS-based car navigation systems.

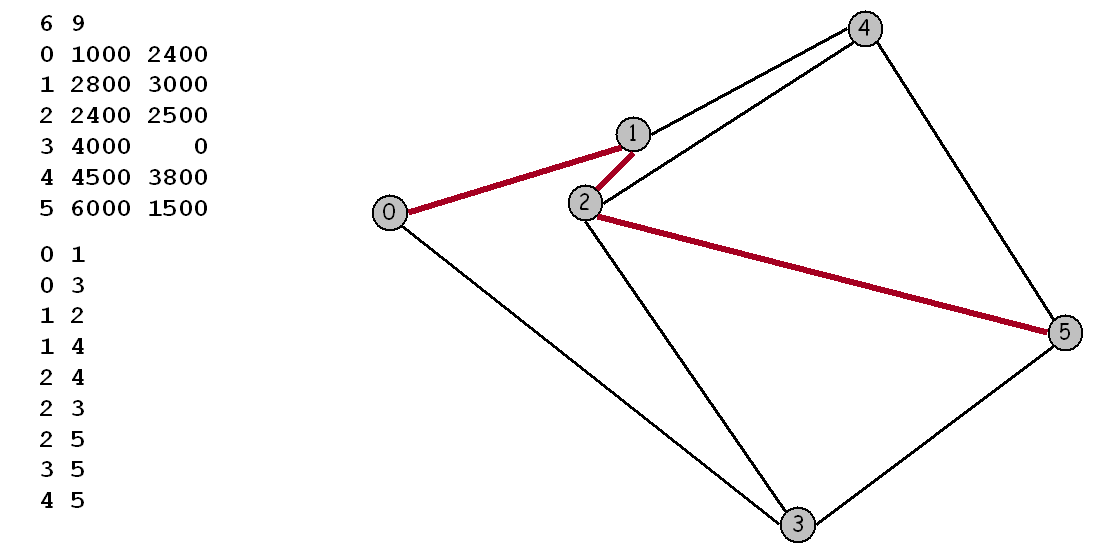
Maps.   For this assignment we will be working with maps, or graphs whose vertices are points in the plane and are connected by edges whose weights are Euclidean distances.  Think of the vertices as cities and the edges as roads connected to them.  To represent a map in a file, we list the number of vertices and edges, then list the vertices (index followed by its x and y coordinates) and then list the edges (pairs of vertices).  For example, input6.txt represents the map below:

Your program should start by prompting the user for the name of an input file that specifies a map. After reading in the map from this file, your program should prompt the user for a pair of numbers representing the source and destination vertex, and will compute the corresponding shortest path.  For instance, the red edges in the figure represent the shortest path from vertex 0 to vertex 5.

Some Implementation Details.   As you know, I have posted an implementation of myWeightedGraph.java that implements edge-weighted graphs and contains an implementation of Dijkstra's shortest path algorithm. Furthermore, this implementation allows you to assign (x, y) coordinates to each vertex. You will notice two additional data members:

	protected double[] x;		// 1-d array to store x-coordinates
	protected double[] y;		// 1-d array to store y-coordinates

        public void addVertex(String newVertex, double xcoord, double ycoord)

Your goal.   Your eventual goal is to run Dijkstra's algorithm on a map with 87,575 intersections (vertices) and 121,961 roads (edges), provided in the file usa.txt. Since the graph is fairly large, you will have to optimize Dijkstra's algorithm. I tried out the current implementation of Dijkstra's algorithm and the myWeightedGraph class on usa.txt. It took about 10 minutes to build the graph and 428,193 milliseconds (i.e., about 428 seconds = 7 minutes) to answer a shortest path query from vertex 0 to vertex 80,000. Imagine trying to use Google Maps to figure out a shortest car route from Iowa City to Princeton - the response is pretty much instantaneous! While your program's response time need not match Google Maps, it would be wonderful if it could answer shortest path queries in a few seconds (how about 10 seconds?), rather than in a few minutes.

Once you read in (and optionally preprocess) the map, your program should solve shortest path problems in sublinear time, that is, in time significantly less than the size of the graph.  One method would be to precompute the shortest path for all pairs of vertices; however you cannot afford the quadratic space required to store all of this information. (Make sure you understand the previous two sentences.) Your goal is to reduce the amount of work involved per shortest path computation, without using excessive space.  Here are a few potential ideas that you may choose to implement.  Or you can develop and implement your own ideas.

Idea 1.   You should first make sure that the current implementation of the method DSP is as fast as possible. One source of inefficiency is the getIndex method, which is probably being called many times by DSP. If you replace the current names array that holds the vertices by a hash table (that we used in our projects), then we should be able to improve the overall efficiency of the myWeightedGraph class.

Idea 2.   Let |uv| denote the straight line distance between vertices u and v. The basic source of improvement in Dijkstra's algorithm is the fact that for any vertex v, the quantity |sv| is a lower bound (i.e., less than or equal to) the shortest path distance from the source s to v. This observation allows many optimizations. For example, suppose that we want to compute a shortest path from source s to destination t. Further suppose that at some point in the algorithm, dist[t] is less than or equal to |sv|, for some vertex v. Then, clearly v is not going to play any role (even in the future) in the shortest path from s to t. So we can ignore v from any further computations.

Idea 3.   The naive implementation of Dijkstra's algorithm examines all V vertices in the graph.  An obvious strategy to reduce the number of vertices examined is to stop the search as soon as you discover the shortest path to the destination.  You can use Idea 1 to determine when it is guaranteed that you have a shortest path from s to t, even before you have completely processed the graph. With this approach, you can make the running time per shortest path query proportional to E' log V' where E' and V' are the number of edges and vertices examined by Dijkstra's algorithm.  However, this requires some care because just re-initializing all of the distances to ∞ would take time proportional to V.  Since you are doing repeated queries, you can speed things up dramatically by only re-initializing those values that changed in the previous query.

Idea 4.   Preprocess the graph by dividing it into a W-by-W grid and precompute the distance between each pair of grid cells i and j and use these distances to guide the search. This idea is probably most useful when the source and destination are far apart.

Idea 5.   Many of the vertices have exactly two neighbors. If a vertex v has exactly two neighbors u and w, then you can replace the two edges u-v and v-w with a single edge u-w whose length is the sum of the lengths of the two original edges. This reduces the number of vertices and edges in the graph. The main challenge here is to print out the shortest path in the original graph after you've compute the shortest path in the reduced graph.

Testing.   The file usa.txt contains 87,575 intersections and 121,961 roads in the continental United States.  The graph is very sparse - the average degree is 2.8.  Your main goal should be to answer shortest path queries quickly for pairs of vertices on this network.  Your algorithm will likely perform differently depending on whether the two vertices are nearby or far apart.  We provide input files that test both cases. You may assume that all of the x and y coordinates are integers between 0 and 10,000.

What to submit.   Use the name map.java for the program tha reads usa.txt, builds an edge-weighted graph, and then interacts with the user to obtain source-destination pairs to find the shortest path between. Submit the files map.java, myWeightedGraph.java, and any other java programs that the myWeightedGraph class depends one.

To get credit for the homework, you should submit all versions of your programs, each version in a separate directory. The expectation is that each version is an improvement over the previous version in terms of efficiency. In each version directory, please a README text file that specifies exactly what "tricks" you used in the current version to improve its efficiency.

You will get full points for the homework, if you implement Idea 1 and a simple version of Idea 2 that makes permits the shortest path algorithm to terminate without processing the entire graph. More sophisticated version of Idea 2 and Ideas 3-5 can go into subsequent versions and you will get extra credit for successful implementation of these ideas. Anything you can come up with is also par for the course.