int[] A = new int[5]; // A is an integer array with five elements
for(int i = 0; i < n; i++)
{
if(i == A.length)
A = resize(A, A.length+1);
A[i] = 10;
}
-
What is the running time of this code fragment, as a function of
n?
Express your answer using the "Big Oh" notation.
For partial credit, make sure that you show how you derived your answer.
Solution: O(n^2).
For values of i = 0, 1, 2, 3, and 4, each execution of the body of the for-loop takes a constant, say c, number of steps because the condition in the if-statement evaluates to false. For values of i, greater than 4, each execution of the body of the for-loop takes time proportional to i. This is because the condition inside the for-loop evaluates to true and the call to the resize function, which resizes A from size i to size (i+1), takes time proportional to i. Thus the total running time is:O(1) + (5 + 6 + ... + n-1) = O(n^2)
- Making a tiny change to the above code fragment will bring its running time down, dramatically. What is this change? What will the new running time be, as a function of n, in "Big Oh" notation?
Solution: There are two different changes we could make to get the running time of the code fragment down to O(n). Either of these changes is a correct answer to this question.
- Since n is known, we can replace the definition of A by
int[] A = new int[n]
If we do this, then no calls to the resize function will be made. - Alternately, we could replace the call to the resize function by the following
code.
A = resize(A, 2*A.length);
As discussed many times in class, doing this ensures that we make only a small number of calls to resize and the overall running time is O(n).Notes: If you want to look at the code for a specific resize function, see the end of the exam.
- Depth first traversal.
Here is incomplete code for a method of the myGraph class
called allConnected.
For each pair of vertices u and v in the graph,
the function prints out a message indicating whether
the vertices u and v are reachable from each other or not.
The function first calls depthFirstTraversal once, starting from
some arbitrary vertex.
Recall that depthFirstTraversal constructs a data structure
called dFTTree that contains a depth first traversal tree
of the graph.
The function then consults the dFTTree data structure
for each pair of vertices to determine
if they are reachable from each other.
Some important code is missing from the method.
Your task in this problem is to supply the missing code.
public void allConnected() { // Start depth first traversal from the vertex in // slot 0 in the array of Vertices depthFirstTraversal(Vertices[0]); // Generate pairs of vertices for(int i = 0; i < numVertices-1; i++) for(int j = i+1; j < numVertices; j++) { // Use the data structure dFTTree to determine // if vertex i and vertex j lie in the same // connected component or not. There is no need to // call depthFirstTraversal again. // Find the root of i's connected component int rootI = i; while(rootI != dFTTree[rootI]) rootI = dFTTree[rootI]; // Find the root of j's connected component int rootJ = j; while(rootJ != dFTTree[rootJ]) rootJ = dFTTree[rootJ]; // Print message System.out.print(i, j, ":"); if(rootI == rootJ) System.out.println("Reachable"); else System.out.println("Not reachable"); } } -
Recursion.
In Homework 2, you were asked to write a recursive function to generate
all subsets of a given set {1, 2, ..., n}.
In this problem, you are asked to complete a recursive function to generate
all subsets of a fixed size k of a given set {1, 2, ..., n}.
For example, if n = 5 and k = 3, then the output would
consist of the following 10 size-3 subsets of {1, 2, 3, 4, 5}.
1 2 3 1 2 4 1 2 5 1 3 4 1 3 5 1 4 5 2 3 4 2 3 5 2 4 5 3 4 5
Note that the order in which the subsets are generated is not important. Similarly, the order in which elements in each subset are listed, is not important.The function genKSubsets takes two non-negative integers n and k, does some initialization and calls the recursive function recursiveGenKSubsets.
public void genKSubsets(int n, int k) { boolean[] subset = new boolean[n]; recursiveGenKSubsets(subset, n, k); }The code for recursiveGenKSubsets shown below is incomplete. The idea used here is very similar to what is used in generating all subsets of {1, 2, ..., n} (Homework 2). To generate all subsets of size k of {1, 2, ..., n}, first put n into the current subset being generated and generate all subsets of size k-1 of {1, 2, ..., n-1}. Then, skipping over element n, generate all subsets of size k of {1, 2, ..., n-1}. The base cases of the function are shown, but the recursive case is missing some code. Your task is to supply this code.public static void recursiveGenKSubsets(boolean[] subset, int n, int k) { // Base case 1: Since n equals k, the entire set needs to // be generated. Set the remaining elements true and // print out the set. if(n == k) { for(int i = 0; i < n; i++) subset[i] = true; printSubset(subset); return; } // Base case 2: Since k equals 0, it means that the subset // has been completely generated. Set the remaining elements // false and print out the subset. if (k == 0) { for(int i = 0; i < n; i++) subset[i] = false; printSubset(subset); return; } // Recursive case if(k > 0 && n > k) { // Missing code for recursive call 1 subset[n-1] = true; recursiveGenKSubsets(subset, n-1, k-1); // Missing code for recursive call 2 subset[n-1] = false; recursiveGenKSubsets(subset, n-1, k); } } -
Sorting.
Consider Lafore's partition function (Chapter 7, page 328).
Suppose that theArray, which is the array being partitioned,
is the following:
5 1 9 2 11 6
Further suppose that the value of pivot is 4. Show the arrangement of the elements in theArray at the beginning of each execution of the while-true loop.Notes: I have attached a copy of Lafore's partition function at the end of the exam.
Solution: We get to the beginning of the while-true loop only twice and this is how the array looks at each of these instances.
5 1 9 2 11 6 2 1 9 5 11 6
-
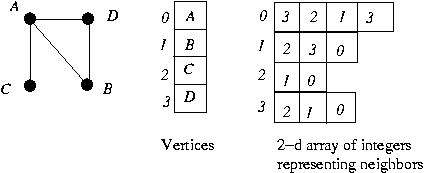
Graph representation.
One way to design a more memory efficient representation of a graph
would be to use a 2-dimensional array of integers, rather than a 2-dimensional
array of booleans. As before, row i of this array would correspond
to the vertex stored in slot i in Vertices.
The first element in this row would be the degree (number of neighbors)
of vertex i.
The remaining elements of the row would be indices of neighbors
of vertex i.
An example is shown in the following figure. The vertex B has index 1 and degree 2. Therefore, the first element in row 1 is 2. This is followed by the indices of the neighbors of B, namely A (index 0) and D (index 3).
The new myGraph class has the following data members. The only difference relative to the original myGraph class is that we are using a 2-dimensional array of integers, rather than a 2-dimensional array of booleans.
String[] Vertices; int numVertices; int numEdges; int[][] Edges; // different from before
Write the implementation of the addEdge function. Assume that it has the following function header.
public static void addEdge(String vertex1, String vertex2)
In the interests of time, do not bother to do any error checking in your function. You may assume that both vertex1 and vertex2 exist and you may also assume that the edge connecting these two vertices does not already exist.Solution: Here is the code for addEdge.
public static void addEdge(String vertex1, String vertex2) { int index1 = getIndex(vertex1); int index2 = getIndex(vertex2); // Add index2 to the row corresponding to index1 // But, first resize the row corresponding to index1, if necessary if(Edges[index1][0]+1 == Edges[index1].length) Edges[index1] = resize(Edges[index1], 2*Edges[index1].length); Edges[index1][Edges[index1][0]+1] = index2; Edges[index1][0]++; // Add index1 to the row corresponding to index2 // But, first resize the row corresponding to index1, if necessary // This is the same code as above, but with index1 and index2 switched if(Edges[index2][0]+1 == Edges[index2].length) Edges[index2] = resize(Edges[index2], 2*Edges[index2].length); Edges[index2][Edges[index2][0]+1] = index1; Edges[index2][0]++; }
The resize function.
// Resizes an array of integers. Can make it larger or smaller,
// depending on what newSize is.
public static int[] resize(int[] data, int newSize)
{
String[] temp = new String[newSize];
int smallerSize = newSize;
if(data.length < smallerSize)
smallerSize = data.length;
for(int i = 0; i < smallerSize; i++)
temp[i] = data[i];
return temp;
}
Lafore's partition function.
public int partitionIt(int left, int right, long pivot)
{
int leftPtr = left - 1; // right of first elem
int rightPtr = right + 1; // left of pivot
while(true)
{
while(leftPtr < right && // find bigger item
theArray[++leftPtr] < pivot)
; // (nop)
while(rightPtr > left && // find smaller item
theArray[--rightPtr] > pivot)
; // (nop)
if(leftPtr >= rightPtr) // if pointers cross,
break; // partition done
else // not crossed, so
swap(leftPtr, rightPtr); // swap elements
} // end while(true)
return leftPtr; // return partition
} // end partitionIt()