22C:21: Computer Science II: Data Structures

Final Exam, 12/15, 2005

This is an open notes/book exam. There are 5 problems, each worth 40 points.

Linked lists. This problem is on Lafore's implementation of the DoublyLinkedList class contains. This appears on pages 226-230 of the textbook. Suppose that we have an application that uses the operations insertFirst and deleteKey from the DoublyLinkedList class. Furthermore, suppose that we know from experience that the calls to the deleteKey operation, made by the application, have a pattern: each key that is deleted is quite "close" (in the linked list) to the most recently deleted key. This problem asks you to modify Lafore's implementation of the DoublyLinkedList class to take advantage of this information and improve the efficiency of deleteKey. Specifically, answer the following two questions.
1. To make the improvement to the DoublyLinkedList class, what data member would you add?
2. Rewrite the deleteKey function so that it is much more efficient. In particular, we want the running time of deleteKey to be proportional to the distance between the key being currently deleted and the key most recently deleted.
The heap data structure. Even though it is convenient to visualize a heap as a binary tree, it is much more convinient to implement it as an array. To understand, this claim better, let us try to implement a binary max-heap as a tree. Let HeapNode be a class with the following data members:
```
	public int iData;
	public HeapNode parent;
	public HeapNode leftChild;
	public HeapNode rightChild;
```
Each node in the heap will be an object belonging to the HeapNode class. The Heap class itself has the following two data members.
```
	protected HeapNode root;
	protected HeapNode lastNode;
```
These two data members are references that provide access to the root (top) of the heap and to the last node in the heap. Let us try to implement the insert function for this new implementation of a heap. Here is an incomplete implementation of the insert function.
```
      public void insert(int key)
      {
	// Creates a new HeapNode object with key in the
	// iData field, and with parent, leftChild, and
	// rightChild, all pointing to null 
      	HeapNode newNode = new HeapNode(key);

	MISSING CODE FOR INSERTING THE NEW NODE
	AS THE LAST NODE OF THE HEAP
      
	trickleUp(lastNode);
      }  // end insert()
```
Supply the missing code for inserting the new node as the last node of the heap. When the heap was implemented as an array, making a new node the last node was simply a matter of assigning the new node to the slot in the array indexed by currentSize. In the current implementation, given the current last node, finding where the new node should go is not as simple.
Dijkstra's Shortest Path Algorithm.
1. Suppose we have a data structure called Magic that provides extremely efficient implementation of all operations one would typically expect of a priority queue. In particular, suppose that Magic provides constant-time implementations of the operations INSERT, DECREASE-DISTANCE, and REMOVE-MIN. What would the running time of Dijkstra's shortest path (DSP) algorithm be, if we implemented it using Magic instead of a binary min-heap? Carefully justify your answer.
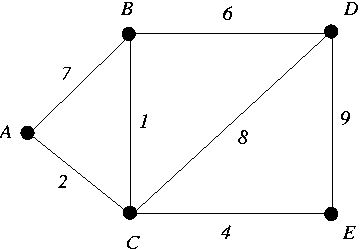
2. Lord Vader returns one last time to tamper with yet another data structure. This time the binary min-heap is the victim! The data structure is tampered so that REMOVE-MIN returns and removes the second smallest element, rather than the smallest element if the heap has two or more elements. Of course, if the heap has only one element, then that is the element returned in response to a REMOVE-MIN operation. For the edge-weighted graph below, show how the Dijkstra's shortest path (DSP) algorithm works when it is run with the tampered heap. In particular show (i) the distance estimates and (ii) the shortest path tree computed by the algorithm.
Binary Search Trees.
1. In this problem, you are asked to implement the left rotation operation on a binary search tree. Specifically, implement a function with the following header:
```
	void leftRotate(Node pivotNode, Node parentNode)
```
  pivotNode is where the rotation takes place; pivotNode can be the left child or the right child of parentNode. The following picture shows a left rotation and clarifies what the above function is supposed to do.
  
  Recall that each Node object in a binary search tree, as implemented by Lafore, contains the following data members.
```
   public int iData;              // data item (key)
   public double dData;           // data item
   public Node leftChild;         // this node's left child
   public Node rightChild;  	  // this node's right child
```
2. Insert the elements 8, 3, 11, 4, 1, 7, in that order, into an empty binary search tree. Show the tree after all the insertions. Delete the elements from the tree in the same order in which they were inserted. Show the tree after each insertion.
Red Black Trees.
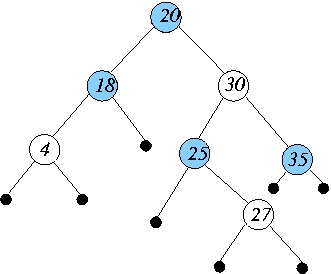
1. Can the nodes of the following binary search tree be colored red/black so that the tree satisfies all the properties of a red-black tree? If your answer is "yes," justify it by showing a valid red-black coloring of the tree. In your answer is "no," provide a small (2-3 sentence) proof.
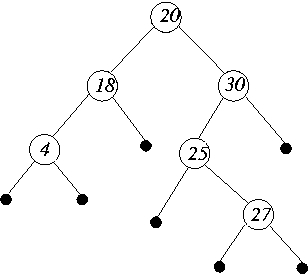
2. Show what happens when the element 26 is inserted into the following red-black tree. The insert operation may run through several iterations before a red-black tree is produced. Make sure you show all of these iterations; also make sure that for each iteration you identify the case (Case 1, 2, or 3) that applies. In the figure below, the shaded nodes are colored black and the rest are colored red.
ENJOY YOUR BREAK