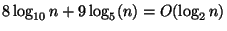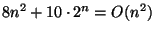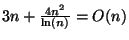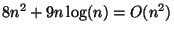22C:21: Computer Science II: Data Structures

Quiz 3: September 24, 2004

  1. For each of the five claims below, write down whether the claim if true or false.
    1. $8\log_{10} n + 9\log_5(n) = O(\log_2 n)$.

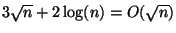
      2. True.
      Explanation: log's of different bases grow at the same rate.
    2. $8n^2 + 10 \cdot 2^n = O(n^2)$.

      3. False.
      Explanation: 2^n grows much faster than n^2 and dominates the expression.
    3. $3n + \frac{4n^2}{\ln(n)} = O(n)$.

      4. False.
      Explanation: n^2/ln(n) grows just a little slower than n^2, but much faster than n.
    4. $8n^2 + 9n\log(n) = O(n^2)$.

      5. True.
      Explanation: n^2 grows faster than n log(n).
    5. $3\sqrt{n} + 2\log(n) = O(\sqrt{n})$

      6. True.
      Explanation: sqrt(n) grows faster than log(n).

  2. The following is a recursive function that determines whether a given integer array is sorted or not. It is missing one line of code, which is a return statement in the recursive case of the code. Complete the function by supplying this missing line of code. 
    public static boolean isSorted(int[] data, int n)
{
	// base case
	if(n == 1)
		return true;
	else
	{
		// Recursive case
		boolean temp = isSorted(data, n-1);
	
		// Here is the missing line of code
		return (temp) && (data[n-2] <= data[n-1]);
	}
}