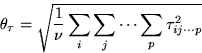Next: References
Up: Help for ANOVA Power
Previous: Effect size random and
In the preceding sections, we have stayed relatively clear of mathematical
notation.
While it is hoped that the ideas are clear, it is probably best to
write this all down notationally and generally in terms of the
standard ANOVA model. The notation here is similar to that in
Kuehl (1994), but similar developments can be found in most general
texts in experimental design, such as Hinkelmann and Kempthorne (1994), Mason et al. (1989),
Montgomery (1997), Kutner et al. (1996), or Winer (1991); or in more advanced
linear-models texts like Christensen (1996), Graybill (1976), or Searle (1971).
Most design texts describe fixed-effects ANOVA models as a sum of
effects that are constrained in various ways. For example, the two-factor
model we have been discussing might be written as follows:
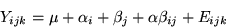
where Yijk denotes the kth observation on the ith row
and the jth column; 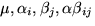 denote the grand mean and effects of rows, columns, and interaction,
respectively; and Eijk is the experimental error associated with
Yijk; these are assumed to be mutually independent and
normally distributed with mean 0 and variance
denote the grand mean and effects of rows, columns, and interaction,
respectively; and Eijk is the experimental error associated with
Yijk; these are assumed to be mutually independent and
normally distributed with mean 0 and variance 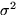 . In the
balanced design, subscripts i, j, and k range over the a rows,
a columns, and n replications in the experiment.
. In the
balanced design, subscripts i, j, and k range over the a rows,
a columns, and n replications in the experiment.
The effects in this model are constrained to sum to zero over
any subscript, holding all others fixed. Thus, in the above model,
we assume that

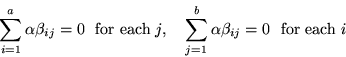
These constraints make all the parameters uniquely identifiable.
The effect SDs are then defined as
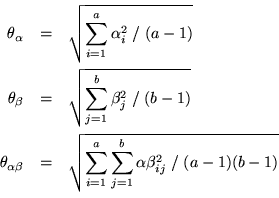
In general, a term 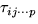 in a fixed-effects model
satisfies the constraint that
in a fixed-effects model
satisfies the constraint that  over
any subscript
over
any subscript 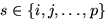 , holding all other subscripts fixed.
The effect SD for this term is defined as
, holding all other subscripts fixed.
The effect SD for this term is defined as
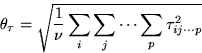
where 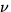 is the associated degrees of freedom.
is the associated degrees of freedom.



Next: References
Up: Help for ANOVA Power
Previous: Effect size random and
Russ Lenth
6/3/1998
![]()

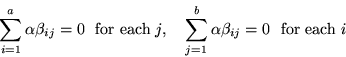
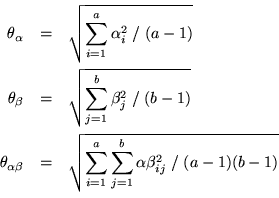
![]() in a fixed-effects model
satisfies the constraint that
in a fixed-effects model
satisfies the constraint that ![]() over
any subscript
over
any subscript ![]() , holding all other subscripts fixed.
The effect SD for this term is defined as
, holding all other subscripts fixed.
The effect SD for this term is defined as