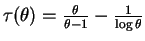- a.
- The joint density of
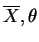 is
is
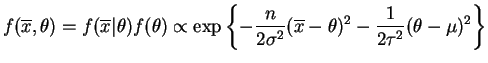
This is a joint normal distribution. The means and variances are![$\displaystyle E[\theta]$](img144.png)
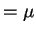
![$\displaystyle E[\overline{X}]$](img146.png)
![$\displaystyle = E[\theta] = \mu$](img147.png)
Var 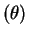
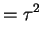
Var 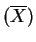
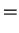 Var
Var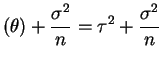
The covariance and correlation areCov 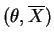
![$\displaystyle = E[\overline{X}\theta]-\mu^{2} = E[\theta^{2}]-\mu^{2} = \mu^{2}+\tau^{2}-\mu^{2} = \tau^{2}$](img154.png)
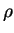
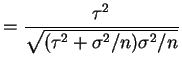
- b.
- This means that the marginal distribution of
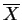 is
is
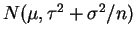 .
.
- c.
- The posterior distribuiton of
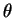 is
is
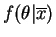
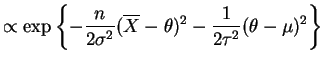
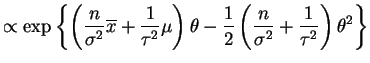
This is a normal distribution with mean and varianceVar 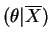
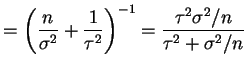
![$\displaystyle E[\theta\vert\overline{X}]$](img164.png)
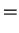 Var
Var
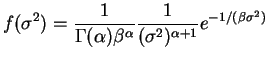 |
The posterior distribution
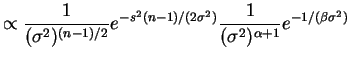 |
||
If
![$\displaystyle = E[1/V] = \int_{0}^{\infty}\frac{1}{v}\frac{1}{\Gamma(a)b^{a}}v^{a-1}e^{-v/b}dv$](img177.png) |
||
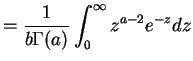 |
||
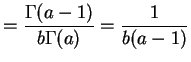 |
So the posterior mean of
![$\displaystyle E[\sigma^{2}\vert S^{2}] = \frac{1/\beta + (n-1)S^{2}/2}{\alpha+(n-3)/2}$](img181.png) |
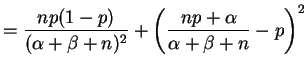 |
||
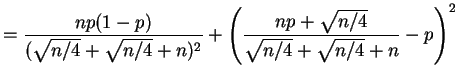 |
||
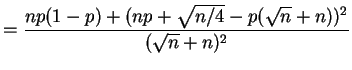 |
||
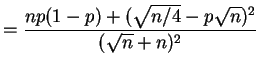 |
||
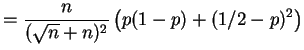 |
||
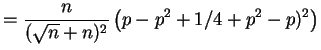 |
||
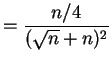 |
which is constant in
- a.
- The population density is
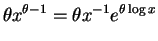
So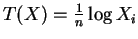 is efficient for
is efficient for
![$ \tau(\theta)=E_{\theta}[\log X_{1}]$](img194.png) .
.
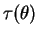

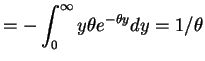
- b.
- The population density is
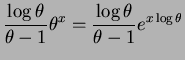
So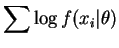
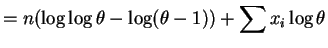
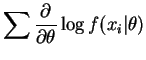
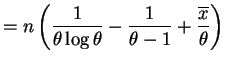
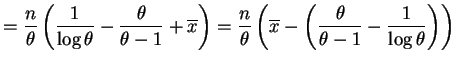
So is efficient for
is efficient for