- a.
- The log likelihood for
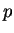 is
is
 const
const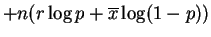
The first and second partial derivatives with respoct to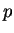 are
are
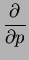
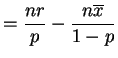
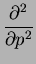

So the Fisher information is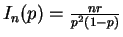 and
the score test statistic is
and
the score test statistic is
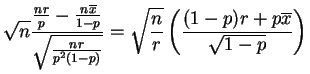
- b.
- The mean is
 . The score statsitic can be
written in terms of the mean as
. The score statsitic can be
written in terms of the mean as
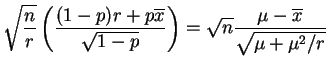
A confidence interval is give by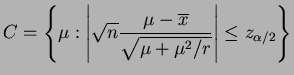
The endpoints are the solutions to a quatriatic,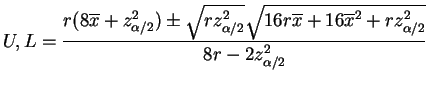
To use the continuity corection, replace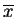 with
with
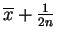 for the upper end point and
for the upper end point and
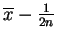 for the lower end point.
for the lower end point.
with the
- a.
- Find the normal equations for the least squares estimators
of
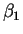 and
and 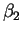 .
.
- b.
- Suppose
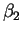 is known. Find the least squares estimator
for
is known. Find the least squares estimator
for 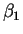 as a function of the data and
as a function of the data and 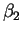 .
.
Solution:
- a.
- The mean response is
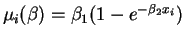 .
So the partial derivatives are
.
So the partial derivatives are
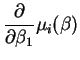
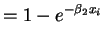
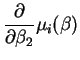
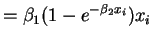
So the normal equations are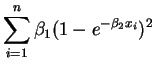
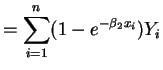
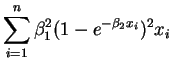
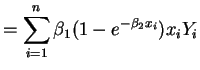
- b.
- If
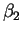 is known then the least squares estimator for
is known then the least squares estimator for
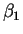 can be found by solving the first normal equation:
can be found by solving the first normal equation:
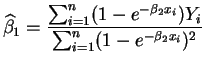
Let
that is,
- a.
- Find the maximum likelihood estimator
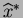 of
of 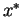 .
.
- b.
- Use the delta method to find the approximate sampling
distribution of
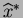 .
.
Solution: This prolem should have explicitly assumed normal errors.
- a.
- Since
 , the MLE is
, the MLE is
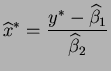
by MLE invariance. - b.
- The partial derivatives of the function
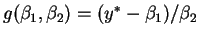 are
are
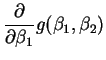

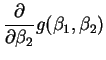
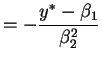
So for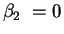 the variance of the approximate sampling
distribution is
the variance of the approximate sampling
distribution is
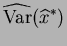
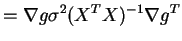
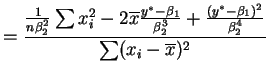


So by the delta method AN
AN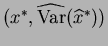 . The approximation is reasonably good if
. The approximation is reasonably good if
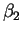 is far from zero, but the actual mean and variance of
is far from zero, but the actual mean and variance of
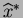 do not exist.
do not exist.
