Also
So
and thus
Equality holds only if
Unconditionally,
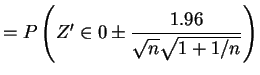 |
||
|
|
- a.
-
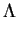
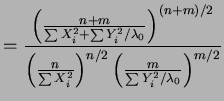
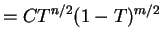
with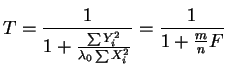
So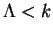 if and only if
if and only if 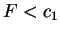 or
or 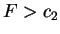 .
.
- b.
-
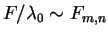 . Choose
. Choose
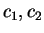 so
so
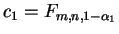 ,
,
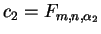 ,
,
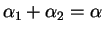 , and
, and
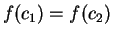 for
for
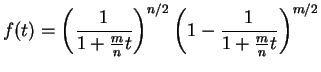
- c.
-
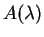
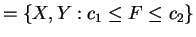
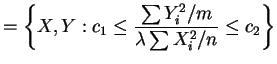
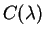
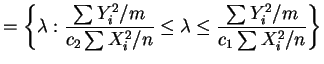
![$\displaystyle = \left[\frac{\sum Y_{i}^{2}/m}{c_{2}\sum X_{i}^{2}/n},\frac{\sum Y_{i}^{2}/m}{c_{1}\sum X_{i}^{2}/n}\right]$](img524.png)
This is a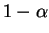 level CI.
level CI.
For the third, look for those ![]() with
with
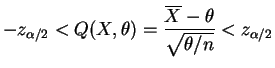 |
If
![\includegraphics[height=2.5in]{week10fig1.eps}](img532.png)
If
![]() , then
, then
![]() is negative with a single mode.
If
is negative with a single mode.
If
![]() is large enough (close enough to zero, then the
confidence set is an interval, corresponding to the two solutions to
is large enough (close enough to zero, then the
confidence set is an interval, corresponding to the two solutions to
![]() .
.
If
![]() is too small, then there are no solutions and the
confidence set is empty.
is too small, then there are no solutions and the
confidence set is empty.
![\includegraphics[height=3.5in]{week10fig2.eps}](img537.png)
- a.
-
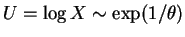 ,
,
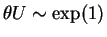 .
So
.
So
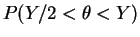
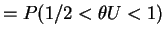
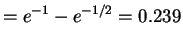
- b.
-
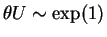 .
.
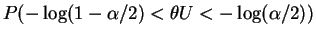
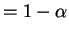
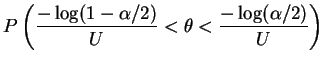
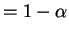
![$\displaystyle [-\log(1-\alpha/2)Y,-\log(\alpha/2)Y]$](img546.png)
![$\displaystyle = [0.479 Y, 0.966 Y]$](img547.png)
- c.
- The interval in b. is a little shorter,
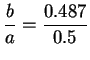
though it is not of optimal length.
