- a.
- The joint PMF of the data is
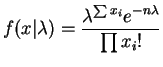
For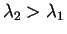 ,
,
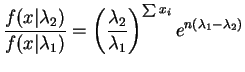
is increasing in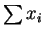 , so has MLR. So a test which
rejects the null hypothesis if
, so has MLR. So a test which
rejects the null hypothesis if
 is UMP of its size.
is UMP of its size.
- b.
- If
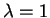 , then
, then
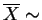 AN
AN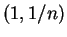 , so
, so
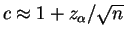 .
.
If
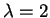 , then
, then
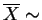 AN
AN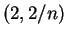 , so
, so
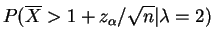
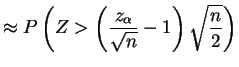
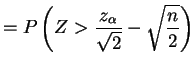
For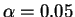 ,
,
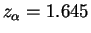 .
.
For
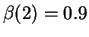 ,
,
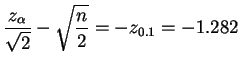
so
so this suggest using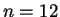 .
.
It might be better to use the variance-stabilizing transformation
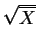 . Either way, use of the CLT is a bit
questionable.
. Either way, use of the CLT is a bit
questionable.
- a.
-
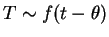 ,
,
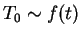 . So
. So
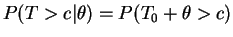
This is increasing in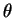 .
.
- b.
- First approach: MLR implies that
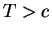 is UMP of
is UMP of
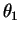 against
against
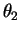 for size
for size
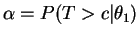 . Since
. Since
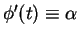 is
size
is
size 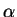 and
and
![$ \beta'(t)=E[\phi'(T)\vert\theta] = \alpha$](img461.png) for all
for all
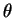 , UMP implies that
, UMP implies that
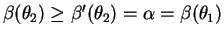 .
.
Second approach: Let
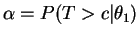 ,
,
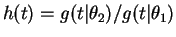 . Then
. Then
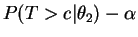
![$\displaystyle = E[\phi(T)-\alpha\vert\theta_{2}]$](img465.png)
![$\displaystyle = \frac{E[(\phi(T)-\alpha)h(T)\vert\theta_{1}]}{E[h(T)\vert\theta_{1}]}$](img466.png)
![$\displaystyle \ge \frac{h(c)E[\phi(T)-\alpha\vert\theta_{1}]}{E[h(T)\vert\theta_{1}]}$](img467.png)
![$\displaystyle = \frac{h(c)(\alpha-\alpha)}{E[h(T)\vert\theta_{1}]}$](img468.png)
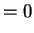
Can also go back to the NP proof.
- a.
- The
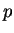 -value is
-value is
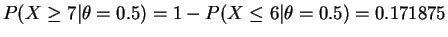 . This can be computed in R with
. This can be computed in R with
> 1 - pbinom(6,10,0.5) [1] 0.171875
- b.
- The
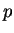 -value is
-value is
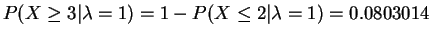 . This can be computed in R with
. This can be computed in R with
> 1 - ppois(2, 1) [1] 0.0803014
- c.
- If
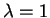 then the sufficient statistic
then the sufficient statistic
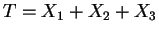 has a Poisson distribution with mean
has a Poisson distribution with mean
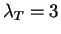 .
The observed value of
.
The observed value of 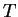 is
is 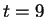 , so the
, so the 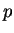 -value is
-value is
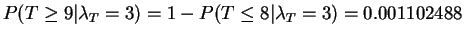 .
.
- a.
- From problem 7.22 the posterior distribution of
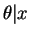 is normal with mean and variance
is normal with mean and variance
![$\displaystyle E[\theta\vert X=x]$](img477.png)
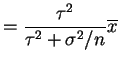
Var 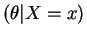
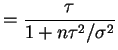
So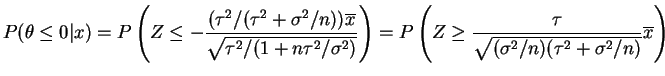
- b.
- The
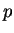 -value is
-value is
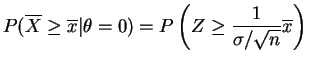
- c.
- For
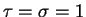 the Bayes probability is larger
than the
the Bayes probability is larger
than the 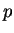 -value for
-value for
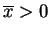 since
since
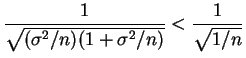
- d
- . As
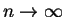 ,
,
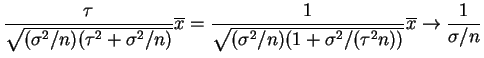
and therefore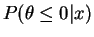 converges to the
converges to the 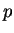 -value.
-value.
