- a.
- The likelihood can be written as
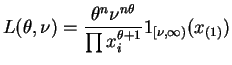
For fixed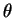 , this increases in
, this increases in 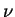 for
for
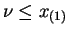 and is then zero. So
and is then zero. So
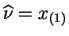 , and
, and
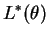
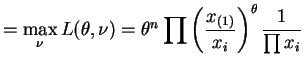
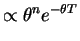
So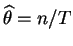 .
.
- b.
- The likelihood ratio criterion is
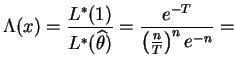 const
const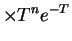
This is a unimodal function of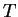 ; it increases from zero to a
maximum at
; it increases from zero to a
maximum at 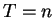 and then decreases back to zero. Therefore for
any
and then decreases back to zero. Therefore for
any 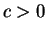
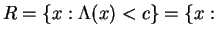
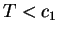 or
or 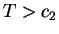
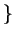
- c.
- The conditional density of
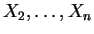 , given
, given 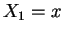 and
and
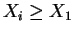 , is
, is
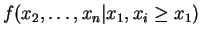
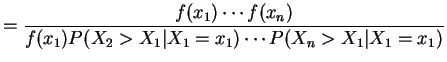
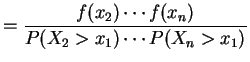
and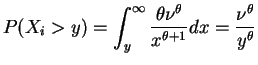
So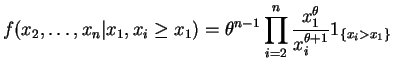
Let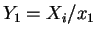 ,
,
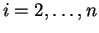 . Then
. Then
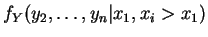
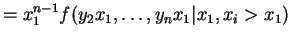
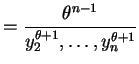
i.e.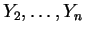 are
are 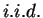 with density
with density
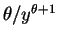 , and
, and
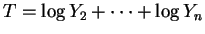 .
.
If
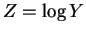 , then
, then
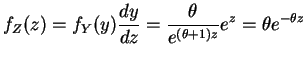
and thus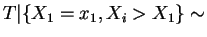 Gamma
Gamma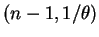 . By symmetry, this means that
. By symmetry, this means that
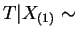 Gamma
Gamma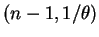 , which is indepentent
of
, which is indepentent
of 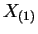 , so
, so 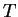 has this distribution unconditionaly as well.
has this distribution unconditionaly as well.
For
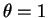 ,
,
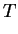
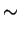 Gamma
Gamma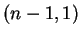
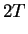
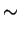 Gamma
Gamma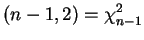
- a.
- The likelihood ratio criterion is
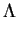
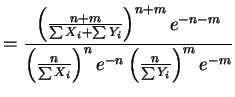
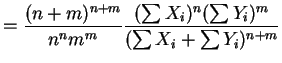
The test rejects if this is small. - b.
- The likelihood ratio criterion is of the form
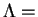 const
const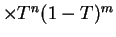 . So the test rejects if
. So the test rejects if 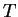 is too small or too large.
is too small or too large.
- c.
- Under
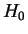 ,
,
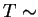 Beta
Beta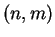 .
.
