; here: R3 = points to savearea.pc
; R4 = M[R3] -- user's pc
; R5 = M[pc] -- fullword
; R6 = ir = M[pc] -- halfword [op2|src|op|dst]
; R7 = src field of IR (IR bits 11 to 8)
; R8 = dst field of IR (IR bits 3 to 0)
ADDSL R7,R3,2 -- get addr of saved src reg
ADDSL R8,R3,2 ; a) (see below) -- get addr of saved dst reg
ADDSI R4,2 -- update copy of usr pc
STORES R4,R3 ; b) (see below) -- store updated pc
LOADS R9,R7 -- get src operand
LOADS R10,R8 -- get dst operand
ADD R10,R10,R9 -- plus operation
STORES R10,R8 ; c) (see below) -- store result
BR INSTDONE
Assume that the preconditions documented above are met. (0.5 points each)
a) The ADDSL instruction on the line marked a) replaces a copy of the 4-bit dst field of the instruction register with what?
___The_address_of_the_saved_dst_reg___________________________
The comments after the double dashes in the code above were inadvertently left in place, making this problem trivial. As a result 3/10 of the class gave decent answers. 3/5 of the class gave odd or nonsensical answers (this ADDSL instruction does not multiply by 5!).
b) If we accidentally omitted the STORES instruction on the line marked b), what behavior change would user programs see?
___An_infinite_loop_because_PLUS_does_not_increment_the_PC____
3/10 of the class got this. 2/5 got partial credit for correctly observing that the program counter was not incremented but failed to relate this to a behavior change that someone trying to debug the program might notice.
c) If we accidentally omitted the STORES instruction on the line marked c), what behavior change would user programs see?
___The_PLUS_instruction_would_not_update_the_dst_register_____
1/2 of the class got this right, while 1/5 got partial credit for stating that it left the wrong value in the dst register (being vague about how it was wrong).
d) With this code, what would be the result if someone wrote this code: PLUS R0,R3
___PC_=_PC_+_R3_______________________________________________
This was harder, only 1/10 got it right and a similar number got partial credit. In the context of this code, examining the code shows that R0 does not mean discarding the result, but rather, it refers to the program counter.
LOADS R3,R4
EXTH R3,R3,R4
A problem: If R4 might not be aligned and we want to the halfword it points to, that is, any two consecutive bytes, we can use the following code, destroying R4. Fill in the blanks to complete it: (1 point)
LOADS R1,R4
EXTB R1,R1,R4 ; get low byte
_ADDSI _R4,1___
LOADS R3,R4
EXTB R3,R3,R4 ; get high byte *
_ADDSL _R3,R1,8 ; combine the bytes
There was an error in the line marked with a *. The code said EXTB R2,R3,R4. This had little impact.
Only 2 students noticed the need for the ADDSI instruction; without it, this code just loads two copies of the same byte, making it useless.
Nobody came up with a compact way to combine the bytes, and most efforts at combining the bytes involved totally inappropriate instructions such as SXT, ORSI or TRUNC. Many who tried to combine the bytes using the wrong instructions also tried to combine them in the wrong order. The Hawk machine stores the least significant byte first!
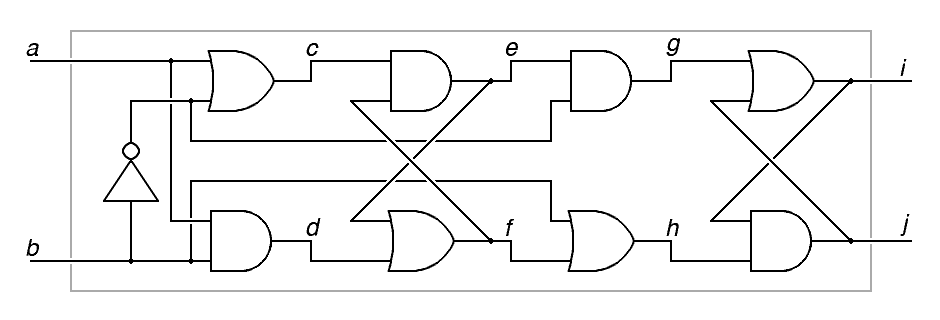
a) Point e will follow changes in point a when point b has what value? (0.5 point)
__1_or True___
The circuit used here was a repeat of the circuit given in Homework 11. As such, it is no surprise that 1/2 of the class got this right.
b) Point i will follow changes in point e when point b has what value? (0.5 point)
___0_or_False_
The second half of this circuit was the mirror image of the circuit from Homework 11, inverting the sense of the clock input. This was not so obvious, so only 2/5 got this right.
c) The data at point a will transfer to point i when point b does what? (0.5 point)
___a_falling_edge_or_a_change_from_1_to_0_______
Only 1/5 got this. The progression of parts a and b lead to this conclusion, but if these were answered wrong, it would be difficult to draw this conclusion.
Note, 1/10 gave an answer on part b) contradicting their answer on part c). These students received only partial credit, since their answer must have been lucky guesswork that was not based on an analysis of the circuit.
ADDSL R3,R3,3 ; \ R3 times 27 = 9 x 3
ADDSL R3,R3,1 ; /
MOVE R1,R3 ; \
ADDSL R3,R1,1 ; | R3 times 27 = 11011
ADDSL R3,R1,2 ; |
ADDSL R3,R1,1 ; /
In contrast, the manual only gives one solution for multiplying by 25:
ADDSL R3,R3,2 ; \ R3 times 25 = 5 x 5
ADDSL R3,R3,2 ; /
A Problem: Give the other solution for multiplication by 25. (1.5 points)
___MOVE____R1,R3________________________________
___ADDSL___R3,R1,1______________________________
___ADDSL___R3,R3,3______________________________
2/5 of the class did well here.
Many students gave excessively complex results, evidence of ad-hoc searches for code to muyltiply by 25 without understanding that both approaches illustrated here have distinct systematic foundations. One alternative is based on multiplying by the factors of the number, the other on adding the partial factors corresponding to the ones in the multiplier.
1/5 gave answers that were too long, some getting the wrong result through remarkable calesthentics. 3/10 gave answers that produced the wrong result, although sometimes using methods that made some sense. Many of these got significant partial credit.
11 10 09 08 07 06 05 04 03 02 01 00 s exp mant
- s -- the sign of the number.
- exp -- the biased exponent, similar to the IEEE system.
- 0000 -- used for non-normalized numbers.
- 1111 -- not a number or infinity.
- 0111 -- the encoding of zero in this biased number system.
- mant -- the mantissa, with a hidden bit as in the IEEE system.
- The point is between the hidden bit and bit 6.
What decimal value is represented by each of the following: (0.5 points each)
a) 001110000000 = ___1.0_______________________________
1/2 got this right, and another 1/10 got partial credit, giving the right answer but for the hidden bit.
b) 101110100000 = __-1.25______________________________
2/5 got this right, and another 1/10 got partial credit, as above.
c) 010100110000 = __11.0_______________________________
3/10 got this right. Errors were difficult to classify, but it is clear that nonzero exponent values are hard.
d) 011100100000 = _160.0_______________________________
3/10 got this right, as above.
e) 001101000000 = ___0.75______________________________
3/10 got this right, as above.
TOINT: ; given: R3 = f, a 12-bit floating point number
; result: R3 = round(f), the nearest integer to f
; uses: R4, scratch register
LEA R4,TABLE
ADDSL R3,R4,2
LOADS R3,R3
JUMPS R1
a) How big (in bytes) is the data structure starting at location TABLE? (0.5 points)
___16K_bytes____________________________________
Just 1 got this right. Most suggested that the table would be from 4 to 16 bytes, few even took the strong hint from the next problem into account. Clearly, they did not understand the algorithm being used.
In explanation: The entire 12-bit number is used as the index into an array of 4096 4-byte integers. That is, the array occupies 16k bytes.
b) Why are the first 128 words of the data structure all zero? (0.5 points)
____The_exponent_for_these_is_0000_(-6)_________
1/10 got this right, and another 1/10 gave vague answers that were worth partial credit. Other ways to express the correct answer would be that the first 128 entries all round to zero.
In explanation: 27 is 128. The first 128 words of the table all hold values with an exponent of 0000. The exponent 0000 means -6 with a hidden bit set to 0 (non-normalized). (The exponent 0001 means -6 with the hidden bit set to 1). As a result, the first 128 values have the form 0.ddddddd × 2-6. Put in conventional form, and these values will look like:
0.000000ddddddd
Such numbers are very small. That implies that their integer equivalents are very small, rounding to zero. In fact, there are quite a few more entries in the table that round to zero before the first entries that round to one.
c) Would this approach work for converting 32-bit IEEE format numbers to integers? Why or why not? (0.5 points)
_____The_table_would_be_16G_bytes_(a_bit_large)_
1/5 got this right. Some got lost in minutia and said that the big problem was the loss of the high bits in the ADDSL instruction. Indeed, these bits are lost, but the reason is that it takes more than 32 bits to address the entire table. On a 32-bit machine, this will not work.
The representation of the 32-bit floating point number is used as the integer index into an array of 4 gigawords. At 4 bytes per word, that is 16 gigabytes, considerably larger than the memory of the Hawk and therefore an impossible conversion algorithm on the Hawk.