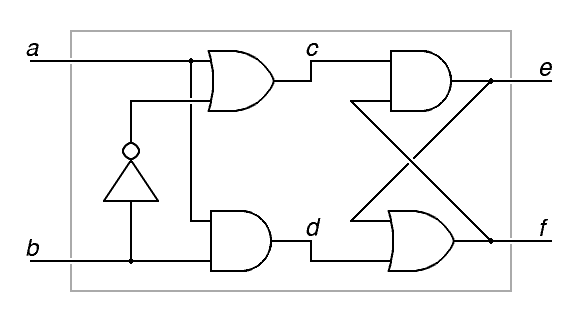
c = a + b
d = a b
e = c f
f = d + e
a) Draw the diagram for this circuit using standard logic notation. Neatness counts. You may want to work out a preliminary version and then redraw it. The inputs a and b should be on the left, while the outputs e and f should be on the right in your final product. (0.4 points)
b) What values should c and d have in order to allow this flipflop to hold a stored value? (0.4 points)
Hold c = true so that e takes its value from f, and hold d = false so that f takes its value from e.
c) What combination(s) of a or b will force c and d to take the values you identified for part b). If one of the variables can be either zero or one, you should not even mention that variable. (0.4 points)
Hold b = false and this will make c true and d false. (When b is false, the value of a does not matter.)
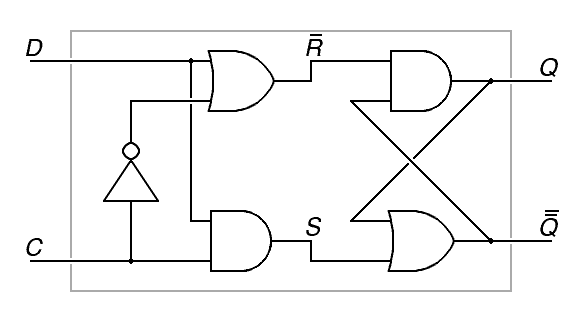
d) This flipflop behaves very similarly to one of the flipflops discussed in the notes. Only one of the inputs or outputs behaves differently. Conventional flipflop inputs, outputs and intermediate points have conventonal labels such as C, D, R, S, R, S, Q and Q. Relate a, b, c, d, e and f to these conventional names in a way that clearly relates this flipflop to the conventional flipflop to which it is most closely related. (0.3 points)
a = D c = R e = Q b = C d = S f = Q̄ We could have said f = Q, but f is not the same as e, so we have tried to render f = Q̄ with a double overbar indicating double negation. This is creative abuse of the standard logic notation for flipflop outputs and not an expected feature of student answers. We could redraw the diagram from part a) as:
- The sparrowhawk.h macros without the STRICTSPARROW restriction. In this case, you have to re-assemble your original program to make it run on the Sparrowhawk.
- A trap handler for the undefined instruction trap on the Sparrowhawk that emulates the missing instructions. In this case, you can assemble your program with hawk.h and then run it on the Sparrowhawk.
a) Given that your Hawk program can be run either way, which approach will give you the fastest execution times? (0.5 points).
Use the sparrowhawk.h macros for speed. This avoids the overhead of interrupt processing and software decoding of the opcode for each virtualized instruction.
b) What limitation does one of these approaches have that causes it to fail to work correctly with some programs? (0.5 points)
The sparrowhawk.h don't always work because they bloat the code by assembling some 32-bit instructions such as LIL in as much as 48 bits (an LIS followed by two ORIS instructions); this can enlarge blocks of code enough that PC-relative branch instructions that worked on the Hawk fail on the Sparrowhawk. (The trap-handler approach does not change the Hawk object code, so it does not suffer from this problem.)
At a very high level, the bus trap handler looks like this:
- Save PC, R1 to R15 and PSW in the trap save area.
- Do something.
- Restore PC, R1 to R15 and PSW from the trap save area in order to return from trap.
In this case, the return from trap will transfer control to the exception handler. The details of how the registers are saved and restored are discussed at length in Chapter 13 of the Hawk manual as well as in Chapter 13 of the notes, but these details do not matter to this question.
A problem: Describe (in a few lines of English text or pseudocode) what the code for the Do something step should do. This must describe how the EXHAND and EXAR fields of the fields of the common block are used. (0.5 points)
We need to load the EXAR field of MEMORY_EXCEPTION into what will be R2 when we return from the trap. To do this, we copy the value into the trap-save-area. Specifically, we copy it into the R2SAVE or svR2 field of the trap-save area (depending on whether you're looking at the course notes or the example code in the Hawk manual).
Similarly We need to load the EXHAND field of MEMORY_EXCEPTION into what will be the program counter on return from the trap. To do this, we copy the value of EXHAND into PCSAVE or svPC in the trap-save area.