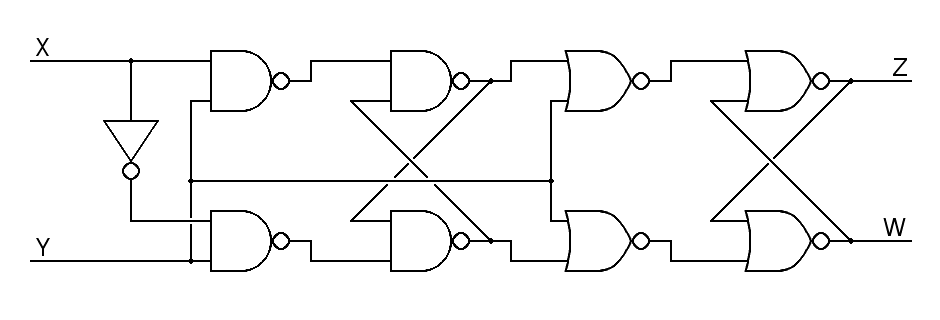
a) Is it edge triggered or just a latch? _Edge_Triggered_
3/4 got this right. Most of the remainder said it was just a latch.
It is obviously a cascade of two D-latch flipflops, so guessing that it is master-slave is reasonable.
b) Which input is the D input? __________X_________
7/8 got this right. Most of the remainder guessed Y.
The X input is inverted on the way to one nand gate, while the Y input goes equally to both nand gates (and 2 nor gates as well), so it has a symmetrical influence on the outputs, making it impossible for it to be a data input.
c) Which input is the C input? __________Y_________
7/8 got this right. Most of the remainder guessed X.
See above. Y having a symmetrical influence on both Z and W, it makes sense to guess that it is the clock or control input.
c) Which output is the Q output? __________Z_________
3/4 got this right. Most of the remainder guessed W.
The X input is inverted an even number of times on the way to Z, so Z will follow X. In contrast, all paths from X to W involve an odd number of inversions, so W will tend to be the inverse of X.
d) What level or edge on the C input can change the output ____falling_edge____
1/2 got this right. 1/8 said rising edge, while 1/10 had answers that did not involve edge triggering. The remainder gave difficult to classify answers.
The left (input or master) stage is a classic textbook D latch that is transparent on a positive clock (Y) input and holds its value when the clock is low. The right (output or slave) stage is built with nor gates. This inverts its behavior with respect to the clock, so it is transparent when the clock is low and holds its value when the clock is high. The result of this combination is that the only time the output can change is when there is a negative-going edge on the clock.
- 00000001 = +0.0078125 (1/128)
- 10001000 = –0.0625 (-1/16)
- 00010000 = +0.125 (1/8)
- 10011000 = –0.1875 (-3/16)
- 00100000 = +0.25 (1/4)
- 11000000 = –1.0
|_|_ _ _|_ _ _ _| s = the sign |_|_|_|_|_|_|_|_| exp = the exponent |s| exp | man | man = mantissa
a) On the above figure of the 8 bits, mark which is the sign bit, which are the exponent bits and which are the mantissa bits. (1.2 points)
3/8 got this right. 1/6 had a 2-bit exponent and a 5 bit mantissa, 1/7 had a 4-bit exponent and a 6-bit mantissa, and 1/14 had a 1-bit exponent and a 6-bit mantissa.
The sign bit was, by design, obvious. Example 4 was crucial to decoding this problem since it is the only one with a value that is not a power of 2. Bit 3 (counting from zero, at the right) must be part of the mantissa for this to work. Either there is a hidden bit, or bit 4 is also part of the mantissa. Examples 5 and 6 are also crucial. These differ by a factor of 4, while the bit pattern (ignoring the sign) is shifted over by just one bit. Therefore, bit 6 is definitely part of the exponent. In example 6, if the exponent is only one bit, then the mantissa is all zero, yet the value is not zero. Therefore, a one-bit exponent would require that there be a hidden bit that is 1 when the exponent is 1 and zero otherwise. This leads to the hypothesis of a 1-bit exponent that several students proposed, but the use of a hidden bit requires that the two lowest exponent values (the only two exponent values) be used to control the hidden bit and have the same numerical interpretation. The net result is as if the number was a simple fixed point fraction, in which case the value of example 6 would have to be 1/2 to match up with the value of example 5. The only surviving hypothesis is that the exponent is 3 bits with a 4 bit mantissa and a hidden bit.
b) Which of the above example values are not normalized? ______1_and_2_______
(0.4 points)5/8 got this right.
Full credit was given for answers that were consistent with the division between exponent and mantissa proposed in part a).
e) Is there a hidden bit? If so, which exponent value(s)
set it to zero?
___yes___000________
(0.4 points)
1/7 got this right. 1/10 said there was no hidden bit, 1/8 gave really odd exponent values for the values that forced the hidden bit to zero. Fully 1/3 gave answers that could not be classified.
As discussed above, example 6 forces there to be a hidden bit if bit 6 is interpreted as part of the exponent, since the mantissa bits are zero and yet the value is interpreted as being nonzero.
_MOVE_ _R4,_R3_____
_MOVE_ _R5,_R3_____
_MOVE_ _R6,_R3_____
_SR___ _R3,_4______
_SR___ _R5,_12_____
_SR___ _R6,_8______
_TRUNC _R3,_4______
_TRUNC _R4,_4______
_TRUNC _R5,_4______ -- optional
_TRUNC _R6,_4______
1/4 gave good answers. shifts. Random clerical errors were common, but there were some common patterns that were evidence of larger trouble: 1/7 made no effort to truncate, 1/10 had no shifts at all, more than 1/20 had trouble with the byte order, as many had trouble with the numbering of bits in a word, and over 1/10 appeared to use random instructions such as LOADS, ADDSL, or EXTB.
In the review session in class, we did the opposite, shifting and masking in order to merge the fields of a floating-point number together. Here, we used shifting and masking to pick apart the fields. Understanding how to do this will be essential to solving Machine Problem 6, although that problem does not require picking apart all of the fields, as was done above.
ADDSL R3,R3,2 ____R3_times_5__________
ADDSL R3,R3,2 ____R3_times_5__________
MOVE R1,R3 ____\___________________
\
ADDSL R3,R1,1 ______R3_times_25_______
/
ADDSL R3,R1,3 ____/___________________
SL R3,4 ____R3_times_16_________
A Problem: What does it do? There is a very short answer: __R3_gets_R3_*_10000__ (3 points)
Note: For partial credit, work out what each piece does and fill in the blanks beside each machine instruction. These blanks will be ignored if your overall answer is correct.
Suggestion: Use scratch paper (or the space below) and see what happens if you start with R3 equal to 1, for example.
The following multipliers were given, most by only 1 student each:
1/65536
1/1000
0.275
125
175
2200
3200
3846
3856
4093
4330
4400 -- by 1/7 of the class
8400
10000 -- by 3/8 of the class
11264
16000
327680A penalty was assessed for wrong answers that did not follow from the work shown above, and a penalty was assessed for failure to multiply out the different factors, for example, for students who gave 25×25×16 instead of 10,000. The popular wrong answer 4400 (and several others) were based on fully understanding all but the 5th line of the code.
Obviously, there was some advantage to having a copy of Chapter 14 of the Hawk manual handy, but merely having done Homework 8 ought to have left enough of an impression that most of this problem could be solved. For those trying to do it by memory, the key question is: Does ADDSL shift before or after it adds, and if before, is it the left or the right operand that gets shifted? (The answer is before, left.)
The mention of foxed-point fractions in the problem statement was a mistake, but of no consequence. Multiplying a fixed-point fraction by 10,000 is no different from multiplying an integer by 10,000.