Assignment 7, Solutions

Part of the homework for 22C:60 (CS:2630), Spring 2013
by Douglas W. Jones
THE UNIVERSITY OF IOWA Department of Computer Science

Background: Consider the problem of converting all upper case text in a string to lower case. A subroutine to do this must look at each character in the string. If the character is upper case, that is, between 'A' and 'Z' inclusive, it can be converted to lower case by adding the constant 'a'-'A'. This works using any character set where the codes for the upper case letters are in alphabetical order, with no gaps, and so aare the codes for the lower case letters.

A problem: Write a subroutine that takes a pointer to a null-terminated string as a parameter and edits that string, converting all upper case letters in that string to lower case. (The string must be stored in RAM, not ROM, for this to be possible. This is not a machine problem. If your code is correct and legible, it will receive full credit even if it is handwritten.) (1.0 points)

; change all upper case letters in string to lower case
;  (note, no activation record is needed here)
TOLOWER:
        ; expects R3 = s, pointer to string
        ; uses    R4    , for packing and unpacking characters
        ;         R5 = ch, the character at *s
TOLOOP:                         ; for (;;) {
        LOADS   R4,R3
        EXTB    R5,R4,R3        ;   ch = *s -- the char pointed to by s
        BZS     TODONE          ;   if (*s == NUL) break

        CMPI    R5,'A'
        BLT     TOENDF
        CMPI    R5,'Z'
        BGT     TOENDF          ;   if ((c>='a')&&(c<='z')) {

        ADDI    R5,R5,'a'-'A'   ;     ch = ch + ('a' - 'A')
        STUFFB  R4,R5,R3
        STORES  R4,R3           ;     *s = ch
TOENDF:
        ADDSI   R3,1            ;   s = s + 1 -- advance to next char
        BR      TOLOOP          ; }
TODONE:
        JUMPS   R1              ; return

Background: Consider this statement in C (or C++ or Java or C#, they all look pretty much the same:
```
        if (!((ch < 'A')||(ch > 'Z'))) ch = ch + ('a' - 'A');
```
A problem: Apply DeMorgan's laws to the Boolean expression on the if statement. The result should be easier to read. (0.2 points)
```
if ((ch >= 'A')&&(ch <= 'Z')) ch = ch + ('a' - 'A');
```
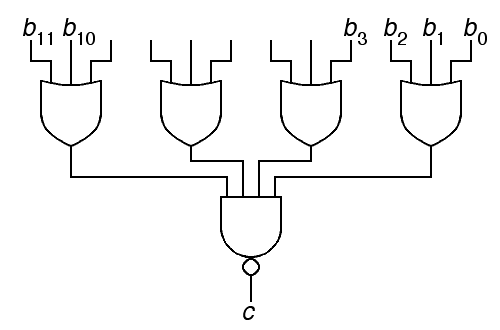
Background: The LOADS instruction sets the C condition code oddly in order to support highly optimized text processing code (a topic discussed in Chapter 7 of the notes). Specifically, the C condition code after a LOADS will be true if any byte in the result is all zero.
To simplify this problem, let's imagine for the moment that the Hawk has a 12 bit word with bits B₁₁ (the most significant bit) through B₀ (the least significant bit). Furthermore, assume that there are just 3 bits per byte, so byte zero consists of B₀, B₁ and B₂, and byte three consists of B₉, B₁₀ and B₁₁.
a) Give a Boolean expression for the C condition code as a function of bits B₀ to B₁₁. (0.3 points)

C = not( (B₀ or B₁ or B₂) and (B₃ or B₄ or B₅)
and (B₆ or B₇ or B₈) and (B₉ or B₁₀ or B₁₁) )
There are, of course, multiple solutions because of DeMorgan's laws.

b) Draw out a schematic logic diagram equivalent to the above. Legibility is important here. If you can't draw a straight line, use a ruler. (0.3 points)
Background: In C or Java, a programmer could write a=b^c to compute the exclusive or of two boolean variables (with values restricted to the range 0 to 1), but beginning programmers sometimes do this:
```
        if (b) a=!c; else a=c;
```
a) Draw a neat and legible schematic logic diagram showing how to compute the exclusive-or of two variables using a 2-input multiplexor and a not-gate. The logic is exactly the same as the code above. (0.3 points)

b) The Hawk has no instruction to compute the exclusive-or of two variables, analogous to the ^ operator in languages like C and Java. Instead, a two-instruction sequence is required to compute this. Give the sequence required to compute R3=R3^R4. (0.3 points)
```
        EQU     R3,R4
        NOT     R3
```
An equivalence circuit outputs true if both of its inputs are the same and false if they are different.
a) (0.3 points) Give the truth table for an equivalence circuit with inputs a and b and output c. (0.3 points)

a b c

0 0 1
0 1 0
1 0 0
1 1 1

b) Use the general methodology for converting any truth table to a logic circuit given in the middle of Chapter 8 of the notes to derive the logic circuit for equivalence from your truth table. (0.3 points)

The above solution is completely un-optimized. Gates 1 and 2 in the and array, for example, are obviously extraneous and can be eliminated.