; activation record format (R2 points to the activation record)
RA = 0 ; the return address
ROW = 4 ; the row number in ARRAY
COL = 8 ; the column number in ARRAY
ARRAY = 12 ; an array of ROWS by COLUMNS integers
ROWS = 3 ; each row is an array of integers
LOG2COLS= 3 ; the whole array is an array of rows
COLUMNS = 1<<LOG2COLS
ARSIZE = ARRAY + ((ROWS << LOG2COLS) << 2)
a) Write code to compute the address of the local variable ARRAY in R3. (1 point)
__ LEA R3,R2,ARRAY _________________
1 in 4 did well here. 1 in 10 earned no credit. Popular errors that earned partial credit were to use the LOAD instruction (to load the first item in the array), or to use the wrong index register as the address of the activation record. 1 in 4 had an answer that was at least somewhat reasonable and then spoiled things by adding extra instructions. 1 in 6 gave good answers that were excessively complex, using multiple instructions.
b) Given that the address of ARRAY is in R3, write code to compute the address of the first element of the array row ARRAY[ROW] in R3. (1 point)
__ LOAD R4,R2,ROW __________________ __ SL R4,LOG2COLS+2 ______________ __ ADD R3,R3,R4 ___________________
1 got this right; 1 in 3 earned no credit. There was a bit of a trick here, many got it right, up to that point. the trick was that each array element is a word, 4 bytes, so the multiplication required is items-per-row times bytes-per-item.
c) Given that the address of the array row ARRAY[ROW] is in R3, write code to compute the address of the array element ARRAY[ROW,COL] in R3. (1 point)
__ LOAD R4,R2,COL __________________ __ SL R4,2 _______________________ __ ADD R3,R3,R4 ___________________
2 did this well, and as above, 1 in 3 earned no credit. Here again, many forgot to multiply by the number of bytes per word.
d) Given that the address of the array element ARRAY[ROW,COL] is in R3, write code to increment the array element ARRAY[ROW,COL] by one. (1 point)
__ LOADS R4,R3 _____________________ __ ADDSI R4,1 ______________________ __ STORES R4,R3 ____________________
1 in 6 did well here, 1 in 4 earned no credit, and the same number omitted any use of load or store instructions.
d) How many columns does the array have? (0.5 points) __ 8 ___________
This was designed as an easy question, and it was. Half got it right. 1 in 15 earned partial credit with the answer 4. The remainder of the class gave odd answers: 1, 3, 6, 9, 24, and 54 all attracted some adherents.
ADDSL R3,R3,2
ADDSL R3,R3,2
ADDSL R3,R3,2
SL R3,3
a) What is the value in R3 at the end of this
computation, as a function of x? (1 point)
__ 1000 ________
Half the class got this, 1 in 8 earned no credit. Common errors included misinterpreted shift counts and problems with algebra.
b) To multiply a value by the constant n on the Hawk, (1) we could factor
n and then multiply by each factor, or (2) we could find all the one
bits in the binary representation of n and then do a shift-and-add
corresponding to each
one bit. Which approach is used above?
(0.5 points)
__ (1) factor __
Half the class got this, half did not. The problem did not lend itself to partial credit and the answer was pretty obvious.
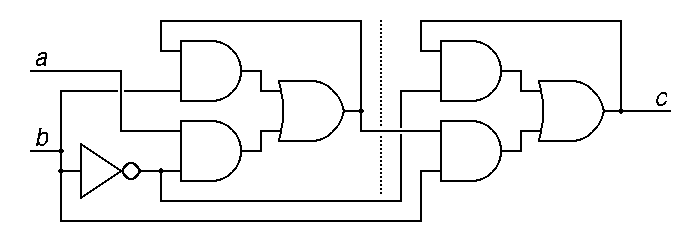
|
a) The above circuit can be made into an edge-triggered master-slave flipflop by the addition of exactly 3 more logic gates, 2 and gates and an or gate. Add these gates and the required interconnections to the figure above. (Suggestion: Use scratch paper to refine your solution before you give your answer in the space above! Hint: A brute-force solution would involve an inverter and a second identical type D latch, but you can always replace two inverters in series with no inverters at all.) (2 points)
1 in 8 gave solutions comparable to that shown above (with the added part being to the right of the dotted line). 1 in 3 earned no credit. 1 in 5 earned good partial credit for following the hint but then making significant errors in optimization. Many had difficulty following the hint.
b) Is the resulting circuit leading-edge triggered
or trailing-edge triggered? (0.5 points)
__ leading _____
Partial credit here depended on an answer to part a) that made at least some sense. 1 in 5 did well.
; fileX.a ; fileY.a
INT B USE "hawk.macs"
EXT A INT A
B: W A EXT B
END C: W B
S .
A: LOAD R1,C
LOADS R1,R1
JUMPS R1
END
a) After fileX.a and fileY.a are assembled and linked (in
that order),
how much memory (in bytes!) is occupied by the combined code
for these two files?
(1 point)
__ 16 __________
1 in 5 did well here; 1 in 5 earned no credit. Students who showed a little of their work so that it was possible to understand what errors they made were more likely to earn partial credit than those who simply gave an un-annotated number. The most common errors were to assume that the LOADS and JUMPS instructions occupied a full word (these are short instructions). Other errors included as allocating space to the INT and EXT directives.
b) What instruction is executed after the JUMPS in fileY.a? (1 point) _ A: LOAD R1,C _
2 in 5 got this. It was difficult to assign partial credit to those whou could not follow this short program.
PKBD: W #FF100000 ; address of keyboard interface
KBDGET: ; link through R1
LOAD R5,PKBD ; R5 = pointer to keyboard interface
KPDPOLL: ; do {
LOAD R4,R5,4 ; R4 = kbdstat
BITTST R4,0 ; -- check the ready bit
BCR KBDPOLL ; } while ((kbdstat & kstatrd) == 0);
LOADS R3,R5
JUMPS R1 ; return kbddata in R3;
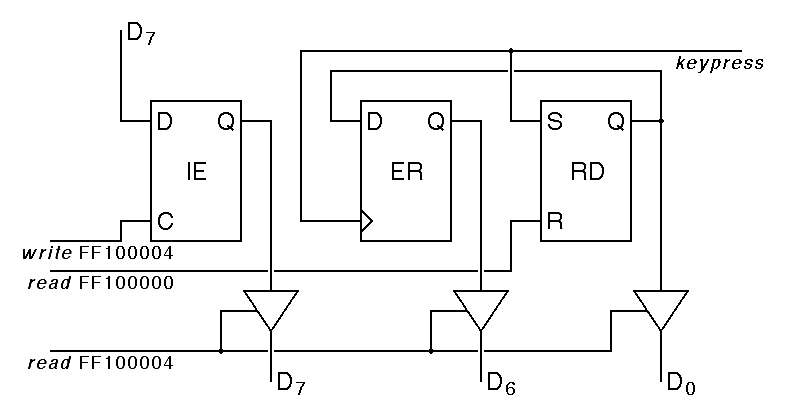
|
a) Assume someone presses a key and holds it down for a while so that the keypress line stays active for a while. What symptoms would you expect with the above hardware and software that would tell you that something was wrong? (1 point)
__ asserting keypress so long as the key is down ________
__ implies that the RD bit will never be reset. The ____
__ result will be read as huge numbers of keypresses ____
1 in 4 gave essentially this answer. About the same number earned no credit for parts a), b) or c).
b) The problem could be solved with a hardware change to the RD flipflop, describe, in English, the behavior that is needed. (1 point)
__ we need some kind of edge triggering so that RD ______
__ is set by pressing (or releasing) the key, not by ____
__ continuing to hold it down. __________________________
1 in 10 got this. 1 in 5 had good ideas that do not work, earning partial credit.
c) The problem could also be solved with a software change to the KBDGET routine. Describe this, in English. (1 point)
__ add a second polling loop to KBDGET to wait for the __
__ key to be released before returning to the user ______
Only 1 in 20 got this. A similar number earned partial credit for answers such as waiting for a delay.
| 31 | 30 | 29 | 28 | 27 | 26 | 25 | 24 | 23 | 22 | 21 | 20 | 19 | 18 | 17 | 16 | 15 | 14 | 13 | 12 | 11 | 10 | 09 | 08 | 07 | 06 | 05 | 04 | 03 | 02 | 01 | 00 |
| page | word in page | byte | |||||||||||||||||||||||||||||
a) Divide the virtual address shown above into
byte-in-word, word-in-page and page fields.
(1 point)
3 in 5 gave the answer shown above. 1 in 8 had answers that were off by one for partial credit. 1 in 10 earned no credit for any part of this problem.
b) How many pages are there in the Hawk virtual address space? (0.5 points) _~1,000,000__
1 in 2 got this.
c) How many frames are there in the Hawk physical address space? (0.5 points) _~1,000,000
1 in 6 got this.
d) If the Hawk page table were stored in a special RAM in the memory
management unit, how many bits per word would this RAM have?
(0.5 points)
__ 20 ______
1 in 14 got this. (Note that all of the arithmetic of finding this answer are identical to the elements of finding the answer above! Both are 220.)
e) If the Hawk page table were stored in a special RAM in the memory
management unit, how many words would this RAM hold?
(0.5 points)
__~1,000,000 ___
1 in 6 got this.
d) If the Hawk page table were stored in a special RAM in the memory
| 31 | 30 | 29 | 28 | 27 | 26 | 25 | 24 | 23 | 22 | 21 | 20 | 19 | 18 | 17 | 16 | 15 | 14 | 13 | 12 | 11 | 10 | 09 | 08 | 07 | 06 | 05 | 04 | 03 | 02 | 01 | 00 |
| exponent | mantissa | ||||||||||||||||||||||||||||||
Both the exponent and mantissa are 2's complement integers, so bits 31 and 23 are sign bits.
a) Give the binary representation of the largest positive number in this number system. (0.5 points)
| 31 | 30 | 29 | 28 | 27 | 26 | 25 | 24 | 23 | 22 | 21 | 20 | 19 | 18 | 17 | 16 | 15 | 14 | 13 | 12 | 11 | 10 | 09 | 08 | 07 | 06 | 05 | 04 | 03 | 02 | 01 | 00 |
| 0 1 1 1 1 1 1 1 | 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 | ||||||||||||||||||||||||||||||
5 of 8 got this right. Those who got it wrong generally assumed that the mantissa was some kind of fixed point fraction instead of reading the explicit statement of the problem that said the mantissa was an integer. A fair number who got this problem wrong simpley looked up some number from the notes (none of the examples there used the representation used for this problem).
b) Give the binary representation of the smallest nonzero positive number in this number system. (0.5 points)
| 31 | 30 | 29 | 28 | 27 | 26 | 25 | 24 | 23 | 22 | 21 | 20 | 19 | 18 | 17 | 16 | 15 | 14 | 13 | 12 | 11 | 10 | 09 | 08 | 07 | 06 | 05 | 04 | 03 | 02 | 01 | 00 |
| 1 0 0 0 0 0 0 0 | 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 | ||||||||||||||||||||||||||||||
Only 1 in 6 got this. The most common errors involved the assumption that the point in the mantissa was somewhere else than at the far right, despite the fact that the problem statement explicitly said tha the mantissa was an integer. Again, a good number copied something from the notes.
c) Give the value of the smallest nonzero positive number in this system, either in decimal or in a concise easy to read algebraic expression. (0.5 points)
__ 1 * 2**-128 _____________________
Only 1 in 20 got this right. Generally, it was impossible to get this right for those who had part b) wrong unless there was very clear documentation of the nature of the false assumptions being made, which was almost never the case. The most notable error here was to assume that the exponent was to the base 10 instead of the base 2. While this was not explicitly stated, none of the binary floating point formats discussed in the notes or in class used base 10, with the exception of scientific notation, which is entirely textual and makes no use of binary representations.
d) Given a number in this format, in R3, write Hawk code to break it into an exponent in R4 and a mantissa in R3. (Hint: You can do this with 4 shift instructions plus some.) (2 points)
___ MOVE R4,R3 ; copy the number ___ ____________________________________ ___ SR R4,12 _____________________ ___ SR R4,12 ; exponent done _____ ____________________________________ ___ SL R3,8 ______________________ ___ SR R3,8 ; mantissa done _____
1 in 8 got this right. Common minor errors included switching the exponent and mantissa (slightly more elegant code was possible with this error, but the problem spec was explicit) or use of unsigned right shifts (you need to sign extend both the exponent and mantissa). Shift counts greater than 16 are impossible on the Hawk, so two shifts are needed to do the 24-bit shift. Off by one errors were common.
Of more concern were students who simply copied from the course notes the code to extract the fields of an IEEE format floating point number. Since the assigned format is not IEEE compatible, that code does not work as an answer to this question!