BCD base 10 excess 3
00100010 22 01010101
01010111 ___57___ _10001010_ *
_10000011_ 83 _10110110_
_10010111_ * ___97___ * 11001010
33 students did well here, and only 3 received under 1/2 credit. The problems marked with stars were the hardest.
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|
| integer part | fractional part |
Fill in the blanks below. In each row, the values are equal; the top
row is worked for you. Round decimal numbers to 3 places after the point.
(2 points)
fixed point binary decimal
0000000000000000100001.0101010101 33.333
1111111111111111111110.1000000000 _____-1.5_____
0000000000000001100100.0000001010 ____100.010___
0000000000001111101000.0000000001 ___1000.001___
1111111111100000101111.1111111101 __-2000.003___
Only one had a perfect score here. The median score for this problem wass 1.2; negative numbers caused problems! Many took the 2's complements incorrectly, producing incorrect fractional parts on the negative numbers. Only 3 had difficulty with the positive integer parts, and only 7 had difficulty with the fractional parts of the positive numbers.
COMMON A,1024*4 (1024 words, 32 rows of 32 words each)
PA: W A
SUBROUT: ; on entry R3 = row
; R4 = column
; on exit, R3-5 wiped out
_LOAD____R5,PA___ ; R5 = A (address of common block)
ADDSL R3,R4,5 ; R3 = word = 32*row + column
_ADDSL___R3,R5,2_ ; R3 = address = 4*word + A
LOADS R4,R3 ; get a word from A
SL R4,1 ; process word
_STORES__R4,R3___ ; return the word to A
JUMPS R1 ; return
What does this code do to the contents of the global variable A? use compact and intuitive C, C++ or Java notation to express this!
_A[row,column]=A[row,column]*2_______________________
6 did well here. The median score was 1.3, and only one student scored below 0.5. 26 students got the first LOAD correct, 21 got the ADDSL correct, only 9 did well with the final STORES, and only 4 gave a good answer to the final question. Partial credit on the final question went to those who understood that this code doubles something and to those who used notation that was far from that of high level languages but still expressed the idea.
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||
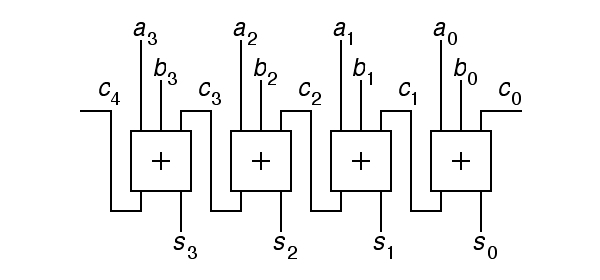
Note! The above circuit is not a full adder! It is something else, even though we used the symbol + to refer to its function in the block diagram. Give the output s and the intermediate values c of this circuit assuming that a=1100, b=0110, and c0=0? (2 points)
s = _0_ _1_ _1_ _0_
c = _0_ _1_ _1_ _0_ _0_
Given your work above, what function does this circuit compute?
_the_difference_a-b_____________________________________
10 did well here, and 10 more gave correct values for s and c; the median score for the problem was 1.4. most of the successful students also wrote in values of s and c on the logic diagram.
; activation record
RA = 0
LOCALA = 4
LOCALB = 8
ARSIZE = 12
; receiving sequence
CODE: ; given R3,R4
; returns R3 = _R3*R4_(the_product)__________
STORES R1,R2 ; _save_return_address_______
STORE R3,R2,LOCALA ; _save_argument_a_(also_xx=a)
STORE R4,R2,LOCALB ; _save_argument_b___________
TESTR R3 ; _test_a____________________
BZS CODEQT ; _if_(a!=0)_{_______________
SR R3,1 ; ___compute_a/2_____________
SL R4,1 ; ___compute_b*2_____________
ADDI R2,R2,ARSIZE ; ___push_AR_________________
JSR R1,CODE ; ___xx=code(a/2,b*2)________
ADDI R2,R2,-ARSIZE ; ___pop_AR__________________
LOAD R4,R2,LOCALA ; ___get_a___________________
SR R4,1 ; ___test_a__________________
BCR CODEQT ; ___if_(a_is_odd)_{_________
LOAD R4,R2,LOCALB ; _____get_b_________________
ADD R3,R3,R4 ; _____xx=xx+b_______________
CODEQT: ; _}_}_______________________
LOADS R1,R2 ; _recover_return_address____
JUMPS R1 ; _return_xx_________________
7 did well here, clearly stating that this code was a multiply algorithm. 3 more gave good comments and relevant but incorrect speculation about its function, and 13 more gave good comments but did not understand the function of the code. Between them, these 23 students represented about half the class and all earned 1.4 points or better.
Generally, those who gave comments at the machine level (R3=R3+R4, R2=R2+12) were less likely to work out what the code did than those who lifted their comments above the machine level (xx=xx+b, push activation record). Generally, those who did not recognize and meaningfully comment on the recursion in this code were also unable to arrive at many other useful comments.